The boundary of a union of spherical balls

We saw that the boundary of a union of sets can be written $$\partial \left( \bigcup_i A_i \right) = \bigcup_i \left( \partial A_i - \bigcup_{j\neq i} A_j \right)$$

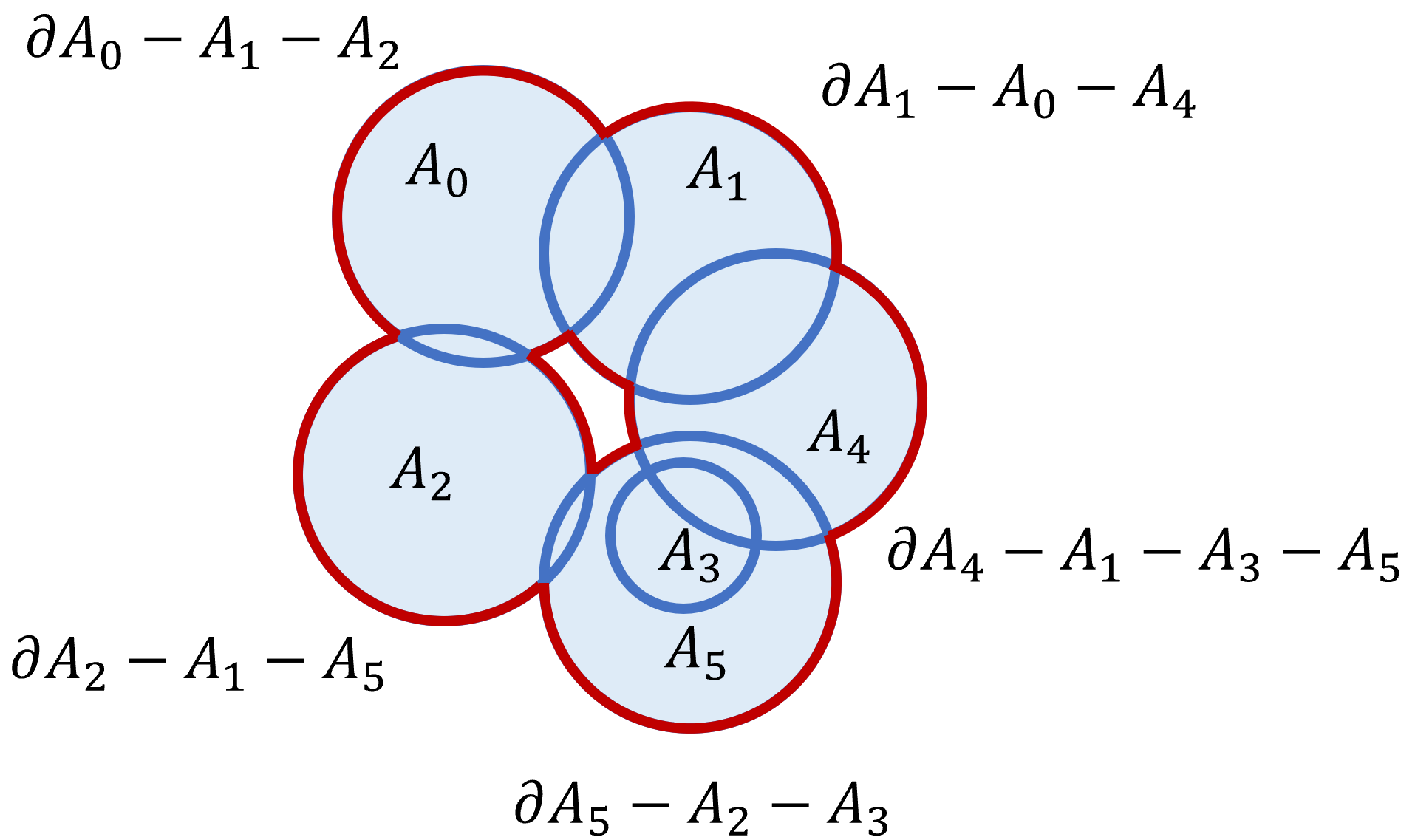
If the sets are spherical balls $$ A_i = B_{R_i}({\bf u}_i)=\left\{ {\bf u}~|~({\bf u}-{\bf u}_i).({\bf u}-{\bf u}_i)\leq R_i^2\right\}$$ the pieces can be represented as the intersection of the sphere with a finite convex polyhedron..

The boundary of a union of spherical balls

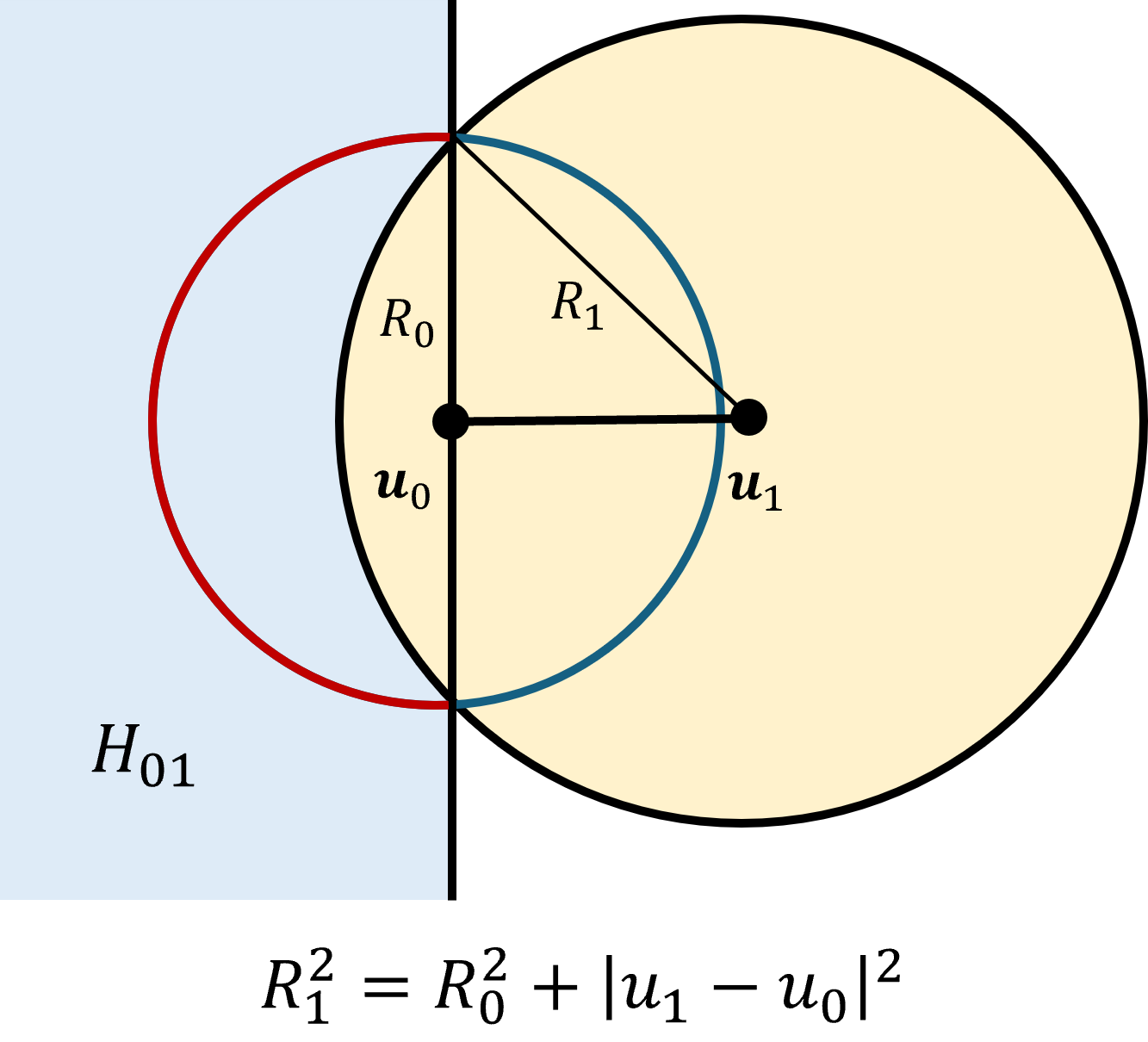
The part of the boundary of a spherical ball $B_{R_0}({\bf u}_0)$ which lies outside another spherical ball $B_{R_1}({\bf u}_1)$ is the set of points $\partial A_0 - A_1 = \partial A_0 \bigcap (\sim A_1)$ $$\begin{matrix} \partial A_0: & ({\bf u}-{\bf u}_0).({\bf u}-{\bf u}_0) = R_0^2 \\ \sim A_1: & ({\bf u}-{\bf u}_1).({\bf u}-{\bf u}_1) > R_1^2 \end{matrix}$$ We can first change origin by writing ${\bf u}-{\bf u}_1 = ({\bf u}-{\bf u}_0)-({\bf u}_1-{\bf u}_0)$. Then, expanding the dot products in the inequality and replacing $({\bf u}-{\bf u}_0).({\bf u}-{\bf u}_0)$ with $R_0^2$ gives $$\begin{matrix} \partial A_0: & ({\bf u}-{\bf u}_0).({\bf u}-{\bf u}_0) = R_0^2 \\ H_{01}: & 2 ({\bf u}_1-{\bf u}_0) . ({\bf u}-{\bf u}_0) < ({\bf u}_1-{\bf u}_0) . ({\bf u}_1-{\bf u}_0) + R_0^2 - R_1^2 \end{matrix}$$ Which is the intersection of the sphere with a half space orthogonal to the line between the centers of the two balls. This is true no matter the dimension of the spheres and is due to the symmetry about that line.

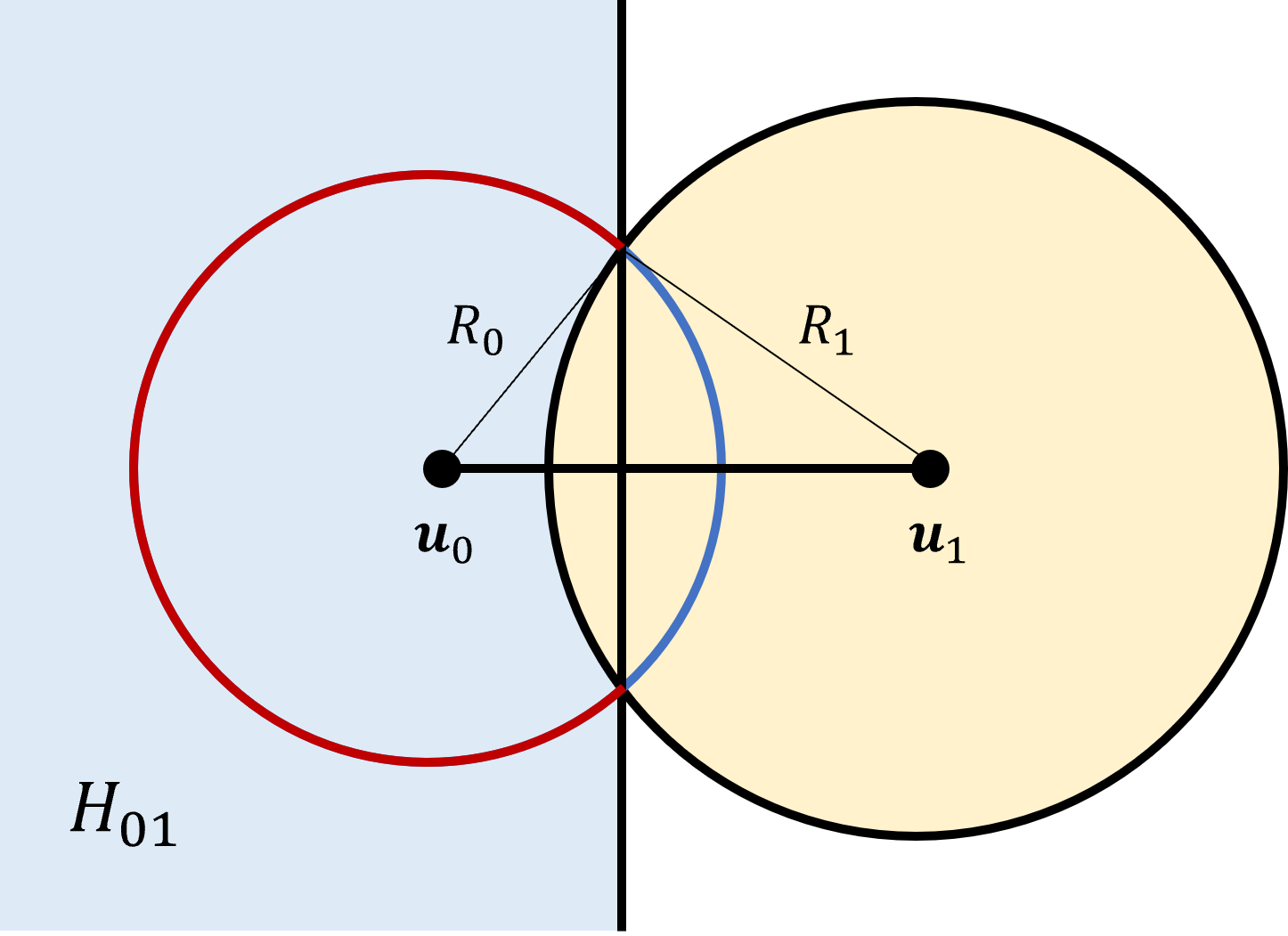
So that's for one pair of balls $\partial A_0 - A_1 = \partial A_0 \bigcap H_{01}$. The next step is to write $$\partial A_i - \bigcup_{j\neq i} A_j = \bigcap_{j\neq i} \left( \partial A_i - A_j \right) = \partial A_i \bigcap_{j\neq i} H_{ij}$$ The last terms are the intersection of half spaces which is a convex polyhedron, which may be infinite.

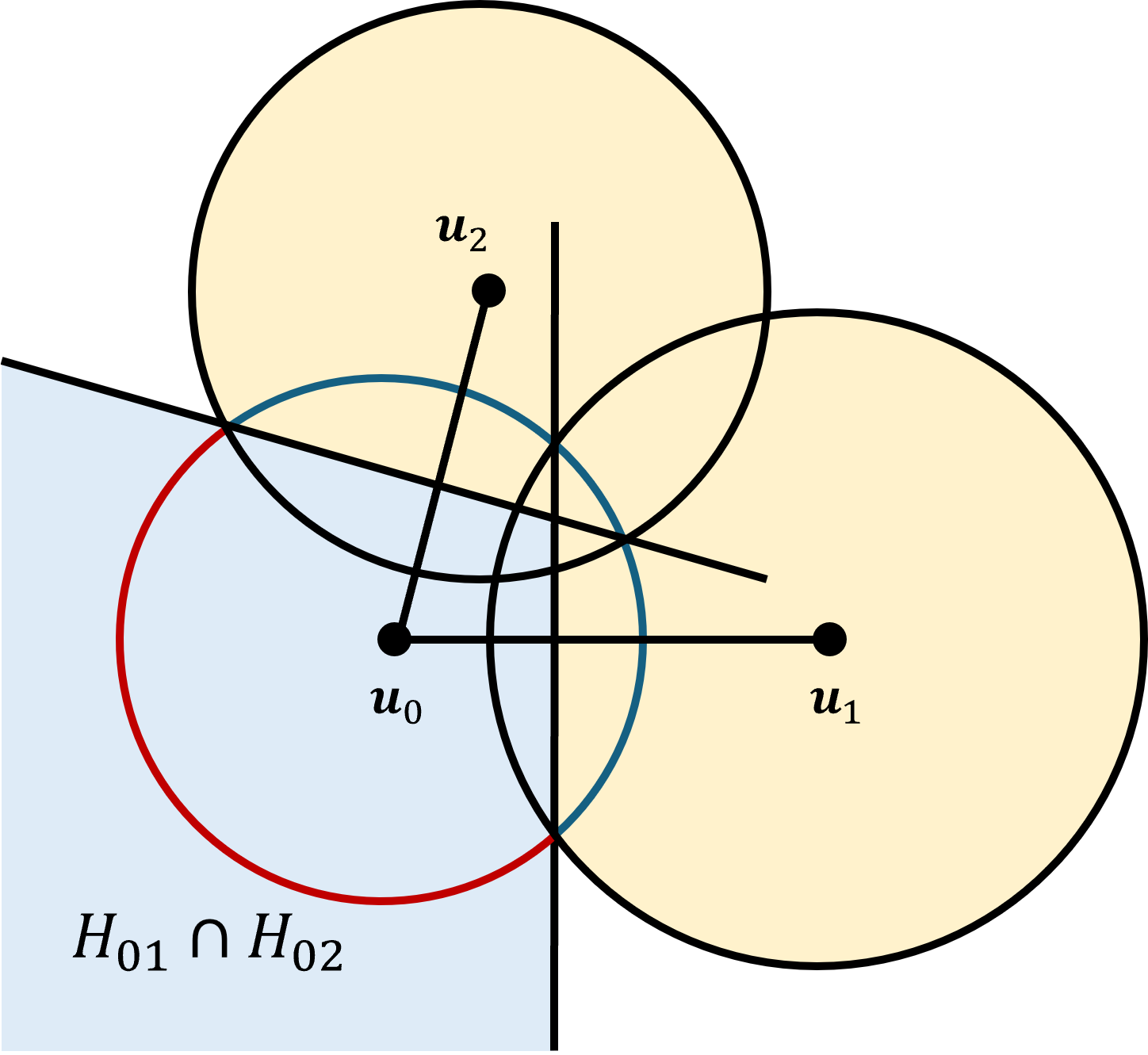
It is easier to deal with finite convex polyhedra, so we are going to introduce a cube $C_i$ centered at ${\bf u}_i$ which strictly contains the original set $A_i$. That is $$ A_i \subset C_i.$$ Including the cube we have $$P_i \equiv C_i \bigcap_{j\neq i} H_{ij}$$

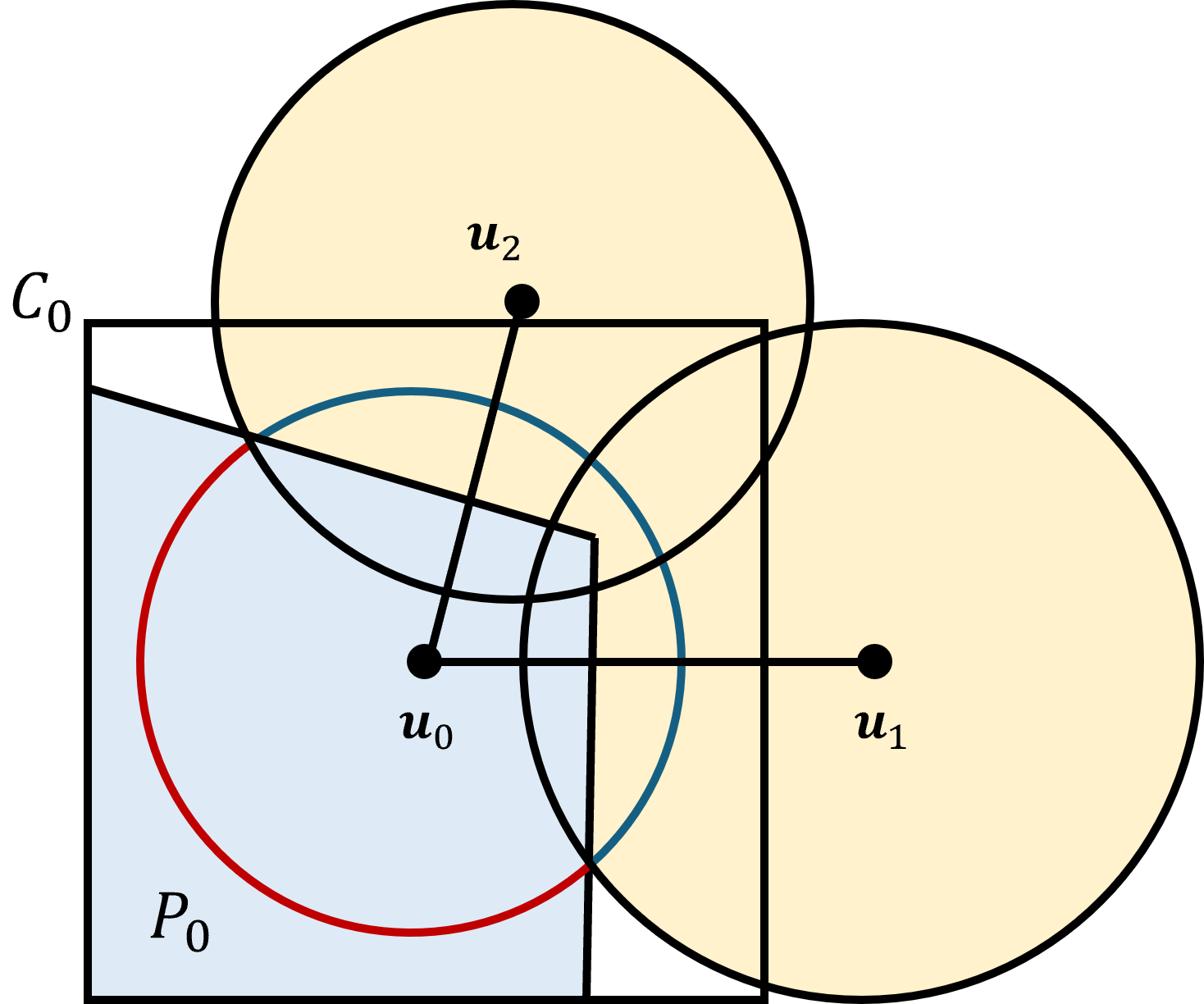
We could use any finite set containing $A_i$, but the cube is itself the intersection of half spaces, which is convenient, and simple in any dimension $k$. Thus $$\partial A_i - \bigcup_{j\neq i} A_j = \partial A_i \bigcap P_i.$$

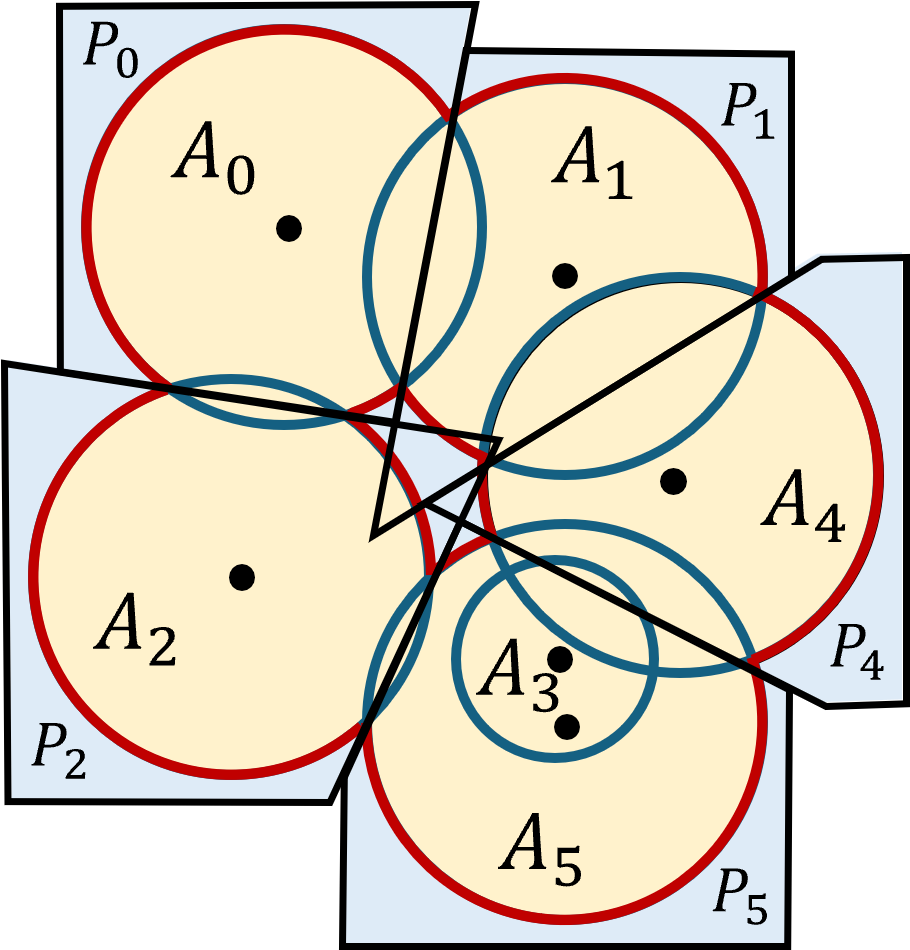
Notice that $P_3$ is empty. While the actual intersection of a sphere and a ball may be empty, the plane is still defined, it moves outside the sphere. To help with intuition, the demo allows you to define your own 2d disks and displays the corresponding polygons. The polyhedra overlap because they were trimmed using only overlapping balls.

This is how it looks in three dimensions. I'd show you four but, you know.

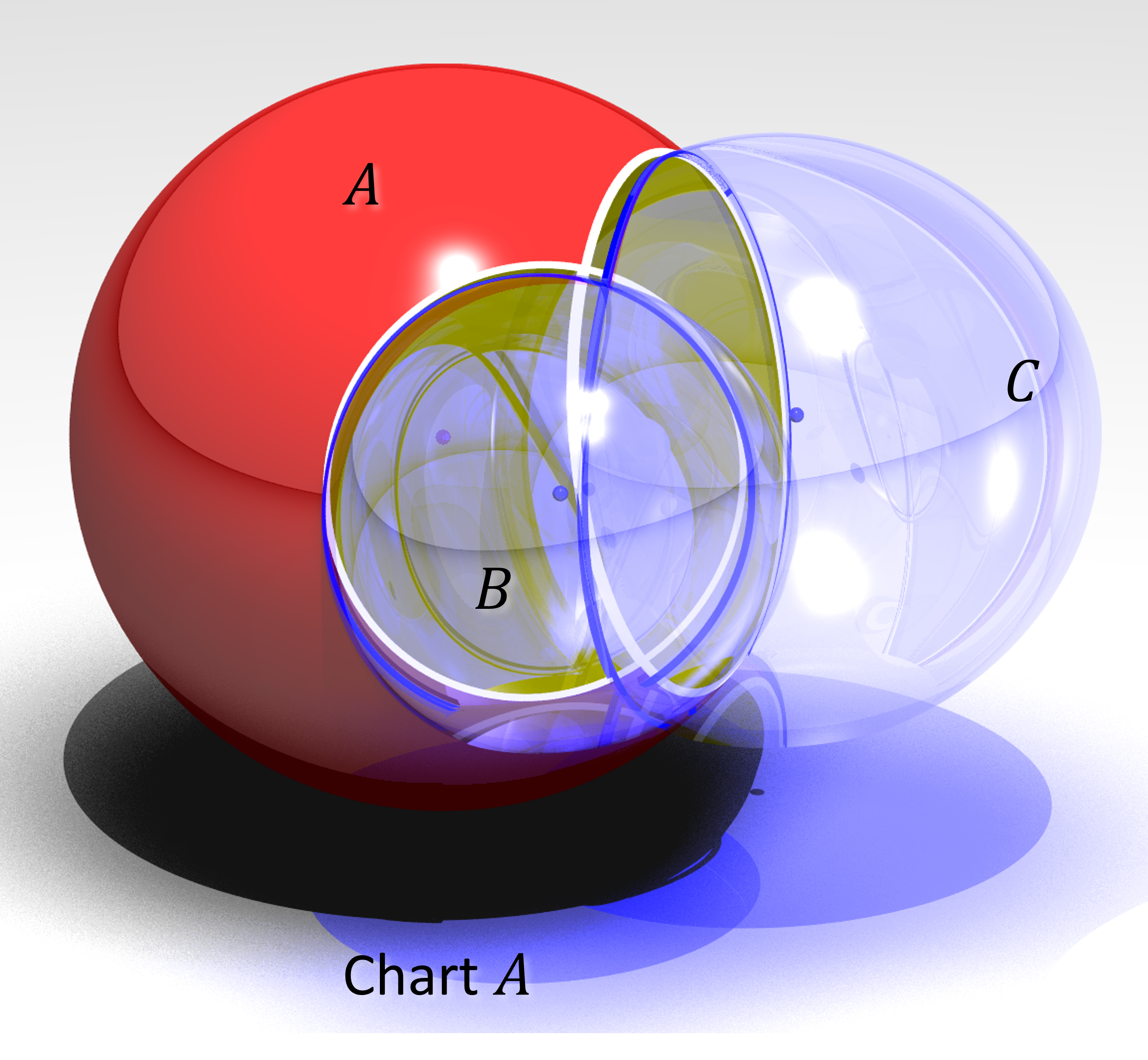
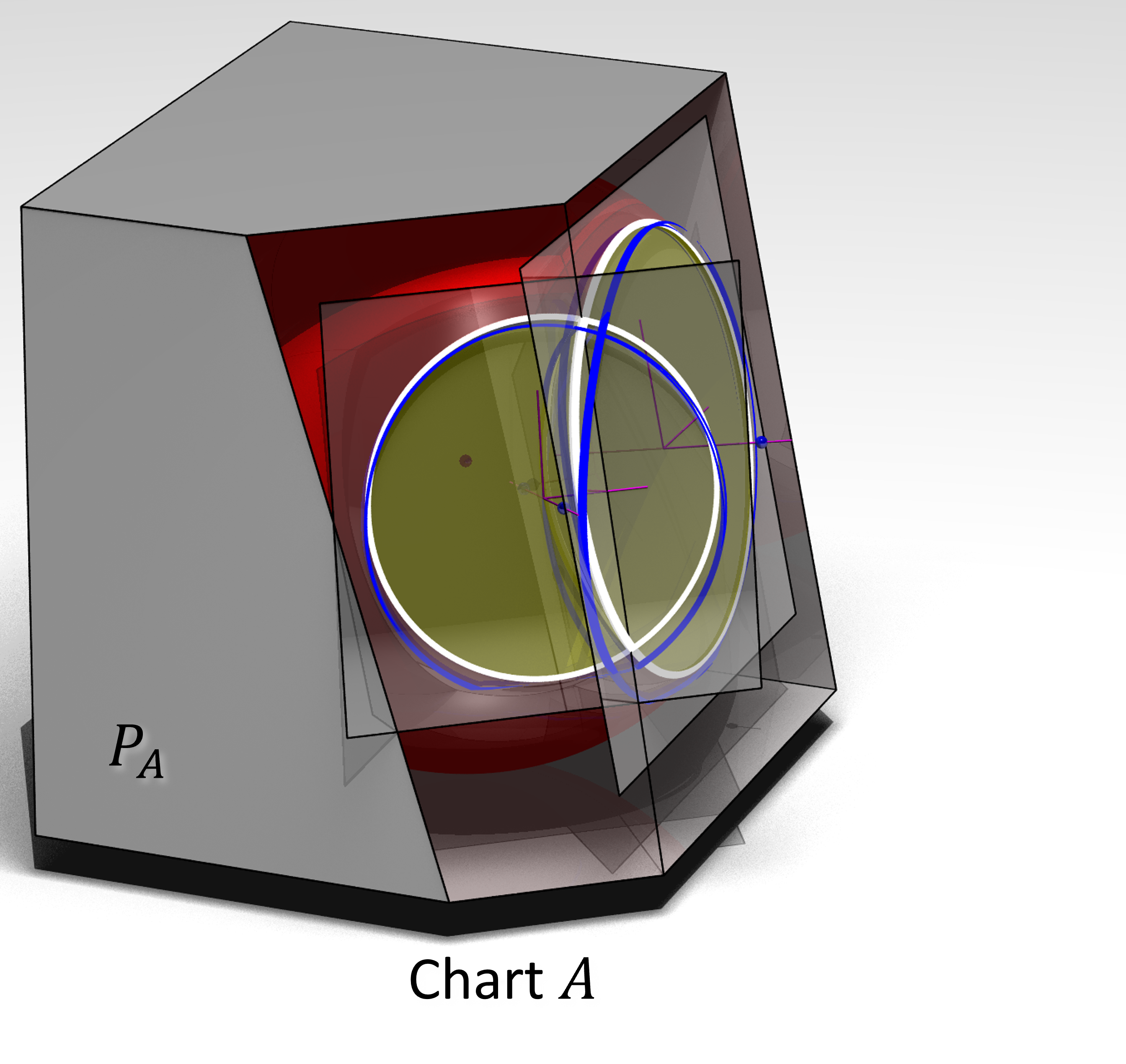
The blue curves reflect the effect of curvature in a manifold, where balls $B$ and $C$ are spherical balls in different tangent spaces.

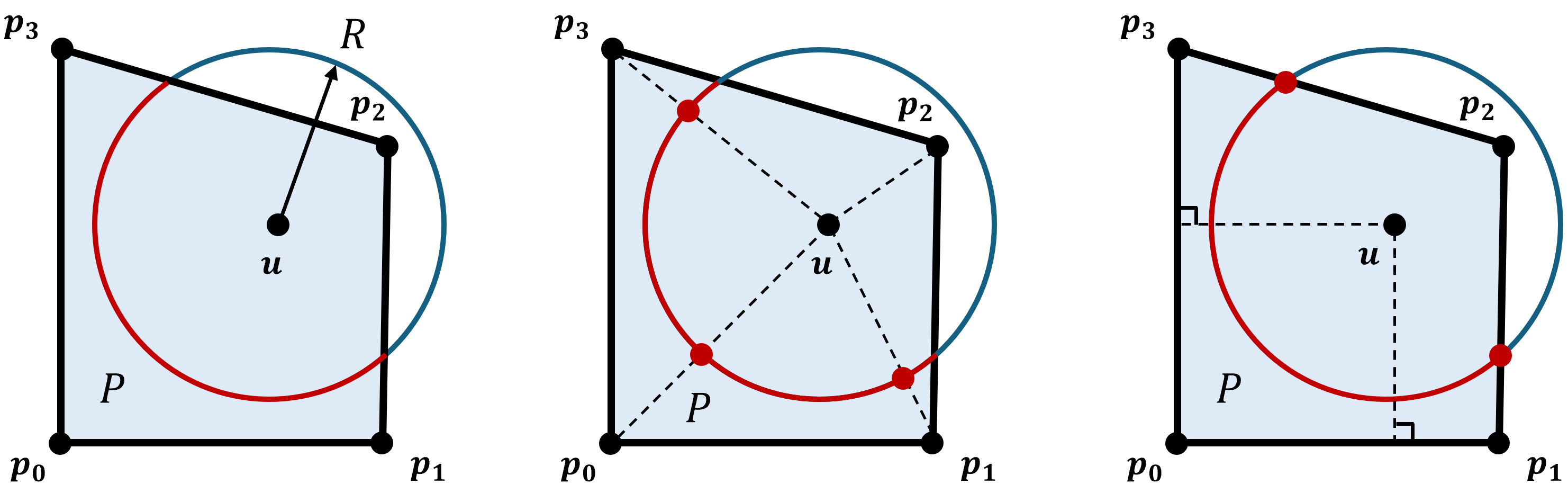
Finding a point on the boundary fragment?

A point on the boundary fragment (the part of the sphere that lies on the boundary of the union of balls) lies on a sphere of radius $R$ and inside the polyhedron $P$. $P$ is finite and convex, so if the vertices of $P$ are ${\bf p}_i$ (relative to the origin of the sphere), any point in $P$ can be written $${\bf s}\in P = \sum \alpha_i {\bf p}_i,\qquad\qquad 0\leq \alpha_i\leq 1,\qquad\qquad\sum \alpha_i = 1 $$ Using the triangle inequality, $${|{\bf s}-{\bf u}|}^2 \leq \sum \alpha_i {|{\bf p}_i-{\bf u}|}^2 \leq \max |{\bf p}_i-{\bf u}|.$$ So if all of the vertices of the polyhedron are inside the sphere, the sphere contributes nothing to the boundary of the union of the balls.

If one of the vertices is outside the ball, there still may not be any points on the sphere that are inside $P$, but if we can find a point in $P$ that is inside the ball a line between that interior point and the exterior vertex has to cross the sphere, and given the two points, finding the point where the radius is $R$ is a matter of solving a quadratic equation (one square root).

There is a hierarchy of points to check, from easy to more complicated. The first is the origin. As the radius of an overlapping ball changes the plane containing the intersection moves along the line between the centers of the two balls. If $R_1^2\leq{|{\bf u}_1-{\bf u}_0|}^2+R_0^2$ for each overlapping ball $B_{R_1}({\bf u}_1)$, the center will be inside the polyhedron. In particular, if $|{\bf u}_1-{\bf u}_0|\geq R_1$ this means that $R_1\leq \sqrt{2} R_0$.

If the center is not in the polyhedron, the next easiest points to find are on the edges of $P$. An edge connecting an interior vertex and the exterior vertex will cross the sphere. Checking for points on faces without an interior vertex requires finding the closest point on a plane to the origin and then checking to see if that point is a convex combination of the vertices. That's more work, but feasible for faces of any dimension. If you've already checked all the lower dimensional faces and they don't contain an interior point this is sufficient.