Manifolds
A manifold is a generalization of the idea of a surface. I'm not certain this is historically accurate, but I think they came cartography, and the problem of mapping the surface of the earth. Think of a chart of part of the world which assigns points on a piece of paper to corresponding points on the earth. These could be represented by a table or a formula giving the point on the sphere (earth) which corresponds to points on the plane (chart). It is common for points on the chart to be measured by geographical coordinates (GCS, or Latitude and Longitude), and then there is an explicit formula (ignoring elevation) for the mapping to the surface of the sphere: $$(lat,long)\longrightarrow R (\cos(long)\cos(lat), \sin(long)\cos(lat), \sin(lat)).$$ This is called a parametric representation of the surface. It gives an expression for the mapping from the chart coordinates to the surface.
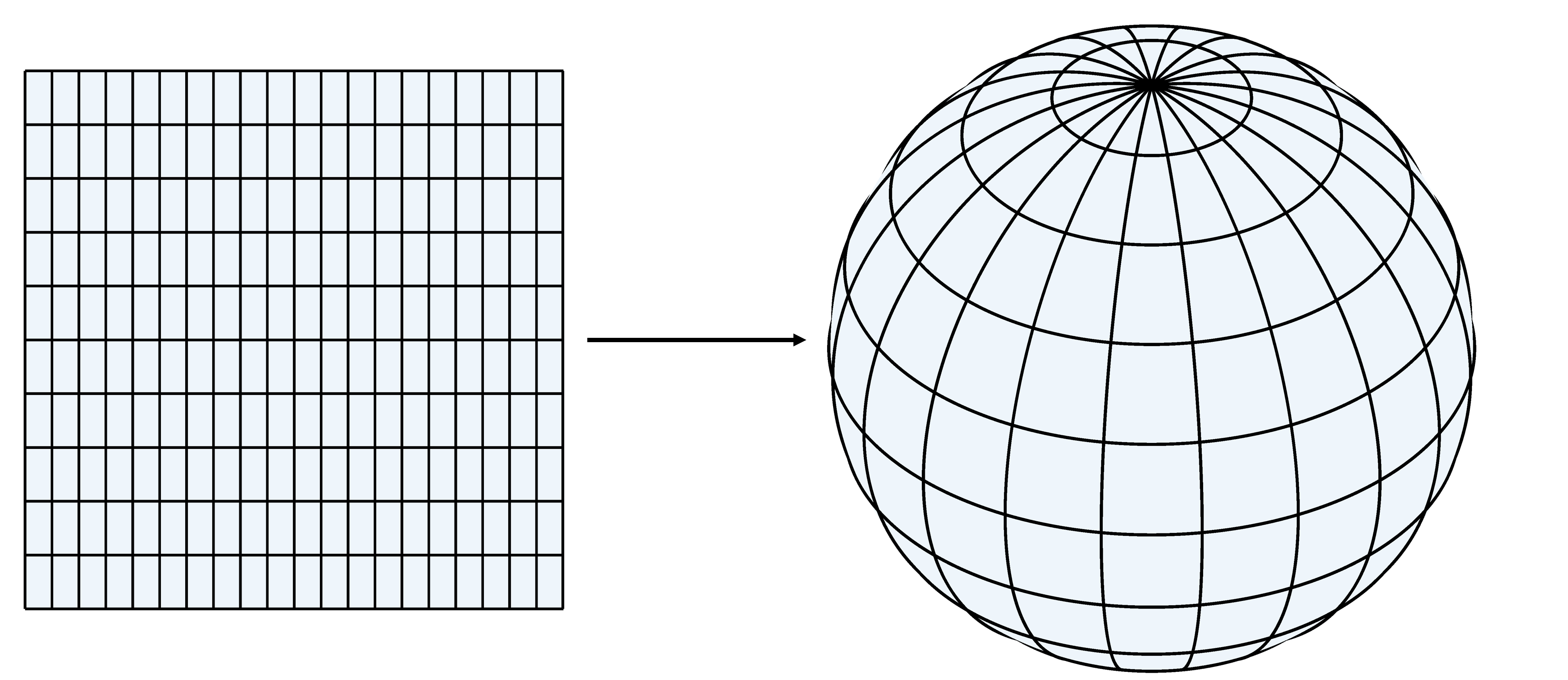
A parametric representation is handy, but it can have problems. A parameterization is "good" if it doesn't distort the picture of the surface. If you draw a small square on the surface, the image of that square in the parameterization should look the same. The length of a step in any parameter direction should be the same length on the surface, and the angle between two directions should be the same.
If the parameterized surface is $$ {\bf u} = {\bf F}({\bf s}),$$ with ${\bf u}\in R^n$ being the point on the surface, ${\bf s}\in R^k$ the parameter, and the mapping ${\bf F}: R^k\rightarrow R^n$ the chart mapping, then a small change $\Delta {\bf s}$ in parameter value becomes a change $\Delta {\bf u}$ on the surface, with $$\Delta {\bf u} = {\bf F}_{\bf u}({\bf s}) \Delta {\bf s}.$$ ${\bf F}_{\bf u}({\bf s})$ is called the Jacobian of the chart mapping. A step in one parameter ($i$) gives a step $$\Delta {\bf u}_i = {\bf F}_{\bf u}({\bf s}) \hat{\bf e}_i,$$ and a "perfect" or Euclidean parameterization would have $\Delta {\bf u}_i.\Delta {\bf u}_i=1$, and $\Delta {\bf u}_i.\Delta {\bf u}_j=0$ is $i\neq j$. In other words $${\bf F}_{\bf u}^T {\bf F}_{\bf u} = I.$$ The displacements $\Delta {\bf u}_i$ are tangent to the surface, and a Euclidean parameterization is one where the tangents are an orthonormal basis for the tangent space.
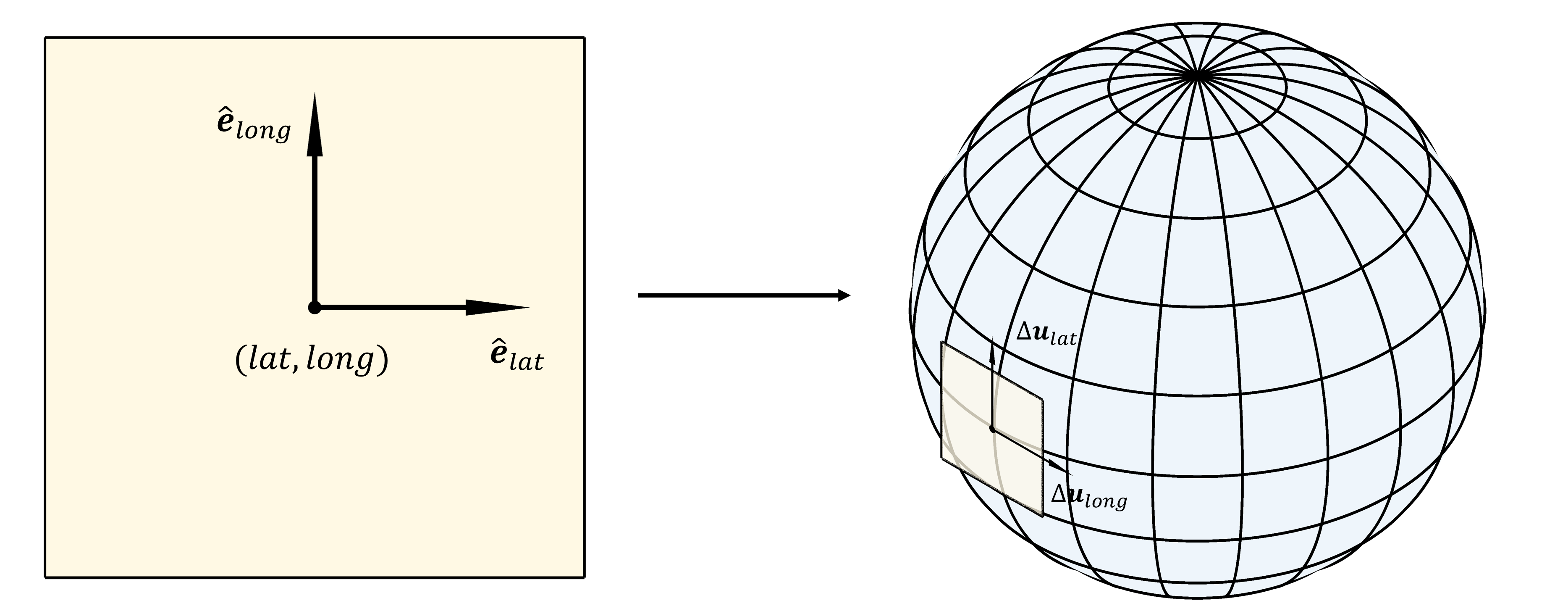
For lat/long parameterization of the sphere the two tangents are $$ \Delta {\bf u}_{lat} = R (-\cos(long)\sin(lat), - \sin(long)\sin(lat), \cos(lat))$$ and $$ \Delta {\bf u}_{long} = R \cos(lat) ( -\sin(long), \cos(long), 0).$$ And so $$ \Delta {\bf u}_{lat}.\Delta {\bf u}_{lat} = R^2,$$ $$ \Delta {\bf u}_{lat}.\Delta {\bf u}_{long} = 0,$$ and $$ \Delta {\bf u}_{long}.\Delta {\bf u}_{long} = R^2\cos^2(lat).$$ Since the scaling by the earth's radius applies equally to both tangents and is the same everywhere it can be forgiven. It is also good that the tangents are orthogonal. However, there is a huge problem at the poles. The length of the longitudinal tangent vector going to zero is what makes it hard to know which direction is north at the poles. (ESRI has a nice description of these issues.)
And exactly how big are Canada and Greenland? They're huge on the map, but that's in the projection (the generalized inverse of the parameterization -- whoa, maybe everything in linear algebra came from cartography too? Nah.). The ratio of area of the image of a small area in parameter space to the original area is the square root of the determinant of the transpose of the Jacobian times itself. So for GCS $$ \left| \begin{matrix} \Delta {\bf u}_{lat}.\Delta {\bf u}_{lat} & \Delta {\bf u}_{lat}.\Delta {\bf u}_{long} \\ \Delta {\bf u}_{long}.\Delta {\bf u}_{lat} & \Delta {\bf u}_{long}.\Delta {\bf u}_{long} \end{matrix}\right| = R^4 \cos^2(lat). $$ One way to fix the equal are problem is to scale latitude by $1/\cos(lat)$. Then the Jacobian is one and areas are preserved. This is the cylindrical or equirectangular projection. It preserves local areas, but not distances. It also makes Canada and Greenland look funny.
It maybe giving cartographers too much credit in the history of mathematics, but trying to fix this little problem at the poles, and more broadly the problem of equal area parameterizations, leads to really important topological and geometric results. Not all surfaces are the same topologically. In general you can't use one parameterization, and you can't in general have parameterizations which are locally orthonormal. (This is like wrapping the surface in paper. You get wrinkles.) That's called a Euclidean metric, and while some two dimensional manifolds like a cylinder or a torus are Euclidean, most are not.
The answer is to define a $k$ dimensional surface to be one which can be parameterized local to any point by an invertible mapping from $R^k$ to the surface. That's a local chart, and objects that have this property are topological manifolds.
In this modern world our GPS shows us a local chart, and it changes as we move along the road or across the sea. But with paper charts you can't do that. Instead a finite set of local charts are bundled into an atlas. If you look at one of these there are small numbers in the margins. Those tell you how to move from one local chart to another. If we move off one chart, we put it away and pick up the one on the page number we get from the spot we left the chart. To be able to figure out where you are on the new chart, you aren't plunked down on the edge of the new chart. There's some overlap so that you can see a neighborhood of where you came from. Continuation Methods are a way to make an atlas of charts.
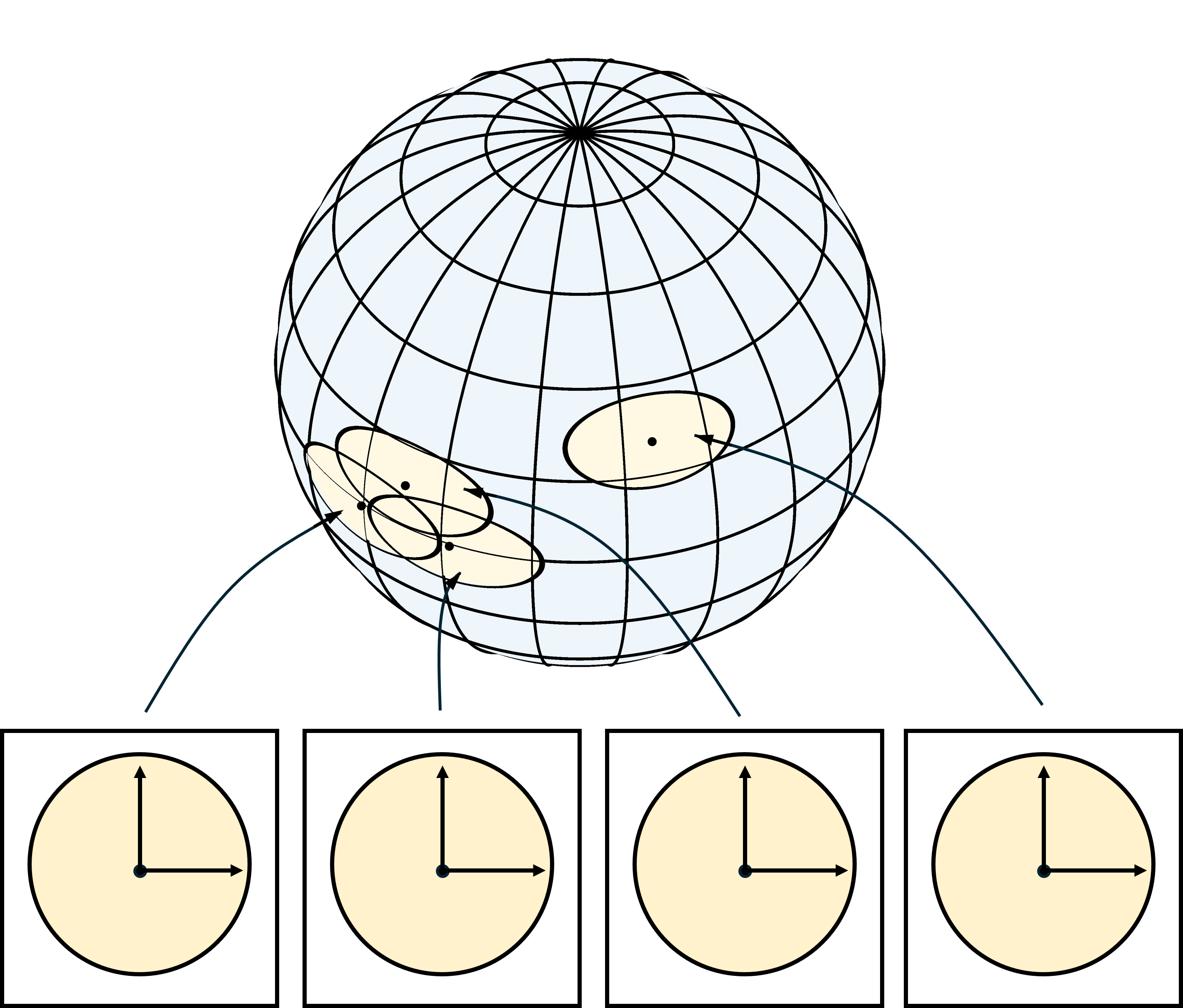
More charts covering smaller part of the manifold also allow us to use charts that are approximately Euclidean. If the partial derivatives of the local parameterization (tangent vectors) are orthonormal and the parameterization projects orthogonal from the tangent space to the manifold the parameterization preserves small distances near the origin.
This is important to mathematics too. It is what connects differential geometry to algebraic topology. A local chart is necessary for navigating, and local charts are necessary for understanding the geometry of a surface. To understand the topology of a surface you ignore the local chart mappings and focus on the information about how the local charts overlap -- the page numbers in the margins. The centers of the local charts in the atlas are a finite set of points distributed on the surface. If two charts overlap the pair of integers which are the chart numbers define an edge between the chart centers. (I'm being a little sloppy, not all overlapping pairs correspond to an edge.) Three charts overlapping define a triangle, four (we're not in two dimensions anymore) define a tetrahedron, and in general $m$ define an $m$ dimensional simplex. Dropping the coordinates of the vertices, this simplicial complex, defined by the overlapping of the charts in the atlas, is an algebraic object that represents the topology of the manifold.
Computationally, a lot has been done with representing, manipulating, and classifying the simplicial complex. Continuation methods for manifolds are a computational technique for finding a finite atlas of charts and the overlap information which defines the simplicial complex.
Interiors, Exteriors and Boundaries
A manifold $M$ is a topological space. The tangent space $R^k$ has a topology of nested open neighoods of any size about each point, and in particular about the origin. Mapping these neighborhoods onto $M$ gives a nested set of open neighborhoods about each point on $M$. This means we can talk about topological concepts like the interior, exterior or boundary of a subset of $M$.
A point in a subset of a topological space is interior to the set if all the points in any neighborhood smaller than some small size are in the set. A point is exterior to the set if no point in any neighborhood smaller than some small size is in the set. A point is on the boundary of a set if every neighborhood smaller than some small size contains both a point in the set and a point which is not in the set.

I've always thought it was fascinating that there is such a simple definition of what is something which is so intuitive. And in such an abstract field as topology.
Dynamics on a manifold
One of the things that helped me in physics classes in college was that I had a lot of math. I remember being giving the homework problem of deriving Newton's laws on a sphere. That can be very messy. Differential geometry provides a way of organizing the problem. Newton's law is $$ {\bf F} = m \frac{{\rm d}^2}{{\rm d} t^2} {\bf r}$$ where now ${\bf F}$ is the force and ${\bf r}$ is the position. In lat/long coordinates a point on the sphere is $${\bf r}= R \hat{\bf e}_r = R (\cos \theta\cos \phi, \sin \theta\cos \phi, \sin \phi).$$ Differentiating w.r.t. time $$\frac{{\rm d}{\bf r}}{{\rm d}t}= \frac{{\rm d}R}{{\rm d}t} \hat{\bf e}_r + R \frac{{\rm d}\phi}{{\rm d}t} \frac{\partial\hat{\bf e}_r}{\partial \phi} + R \frac{{\rm d}\theta}{{\rm d}t} \frac{\partial\hat{\bf e}_r}{\partial \theta}$$ If we stay on the sphere ${\rm d}R/{\rm d}t=0$. We then need to know the derivatives of the basis vector. The normal vector and tangent vectors (differentiate and normalize) are $$\begin{align} \hat{\bf e}_r & = (\cos \theta\cos\phi, \sin\theta\cos\phi, \sin\phi) \\ \hat{\bf e}_\theta & = (-\sin\theta, \cos\theta, 0 ) \\ \hat{\bf e}_\phi & = (-\cos\theta\sin\phi, -\sin\theta\sin\phi, \cos\phi ) \end{align}$$ These are orthogonal, and I have normalized $\hat{\bf e}_\theta$. A little work finds that $$\begin{align} \frac{\partial \hat{\bf e}_r}{\partial \theta} &= \cos\phi \hat{\bf e}_\theta & \qquad\qquad \frac{\partial \hat{\bf e}_r }{\partial \phi} &= \hat{\bf e}_\phi \\ \frac{\partial \hat{\bf e}_\theta}{\partial \theta} &= - \cos\phi \hat{\bf e}_{\bf r} + \sin\phi \hat{\bf e}_\phi & \qquad\qquad \frac{\partial \hat{\bf e}_\theta }{\partial \phi} &= 0 \\ \frac{\partial \hat{\bf e}_\phi}{\partial \theta} &= - \sin\phi \hat{\bf e}_\theta & \qquad\qquad \frac{\partial \hat{\bf e}_\phi }{\partial \phi} &= - \hat{\bf e}_r \end{align}$$ These are the Christofel symbols $\Gamma$. For a Euclidean manifold these are zero (the basis vector don't change as you move). For example $$\begin{align} \frac{\partial \hat{\bf e}_r}{\partial \theta}&\equiv \Gamma^r_{\theta{\bf r}}\hat{\bf e}_{\bf r} + \Gamma^r_{\theta\theta}\hat{\bf e}_\theta + \Gamma^r_{\theta\phi}\hat{\bf e}_\phi\\ \\ & = \cos\phi \hat{\bf e}_\theta. \end{align}$$ And we're off to the races. Substitute to find ${\rm d}{\bf r}/{\rm d}t$, then differentiate again w.r.t. $t$ and substitute again. $$\frac{{\rm d}{\bf r}}{{\rm d}t}= R \frac{{\rm d}\phi}{{\rm d}t} \hat{\bf e}_\phi + R \frac{{\rm d}\theta}{{\rm d}t} \cos\phi \hat{\bf e}_\theta$$ and $$\begin{align} \frac{{\rm d}^2{\bf r}}{{\rm d}t^2}&= R \frac{{\rm d}^2\phi}{{\rm d}t^2} \hat{\bf e}_\phi + R \frac{{\rm d}}{{\rm d}t}\left( \cos\phi \frac{{\rm d}\theta}{{\rm d}t} \right) \hat{\bf e}_\theta + R \frac{{\rm d}\phi}{{\rm d}t} \frac{{\rm d}\hat{\bf e}_\phi }{{\rm d}t} + R \cos\phi \frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}\hat{\bf e}_\theta }{{\rm d}t}\\ \\ &= R \frac{{\rm d}^2\phi}{{\rm d}t^2} \hat{\bf e}_\phi + R \frac{{\rm d}}{{\rm d}t}\left( \cos\phi \frac{{\rm d}\theta}{{\rm d}t} \right) \hat{\bf e}_\theta - R \sin\phi \frac{{\rm d}\phi}{{\rm d}t} \frac{{\rm d}\theta}{{\rm d}t} \hat{\bf e}_\theta - R \frac{{\rm d}\phi}{{\rm d}t} \frac{{\rm d}\phi}{{\rm d}t} \hat{\bf e}_{\bf r} - R \cos\phi \cos\phi \frac{{\rm d}\theta}{{\rm d}t} \frac{{\rm d}\theta}{{\rm d}t} \hat{\bf e}_{\bf r} + R \sin\phi \cos\phi \frac{{\rm d}\theta}{{\rm d}t} \frac{{\rm d}\theta}{{\rm d}t} \hat{\bf e}_\phi\\ \\ &= - R \left( \cos^2\phi {\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2 + {\left( \frac{{\rm d}\phi}{{\rm d}t} \right)}^2 \right) \hat{\bf e}_{\bf r} + R \left( \frac{{\rm d}}{{\rm d}t}\left( \cos\phi \frac{{\rm d}\theta}{{\rm d}t} \right) - \sin\phi \frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}\phi}{{\rm d}t} \right) \hat{\bf e}_\theta + R \left( \frac{{\rm d}^2\phi}{{\rm d}t^2} + \sin\phi \cos\phi {\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2 \right) \hat{\bf e}_\phi \end{align}$$ Notice that if we write the force in the same local coordinate system $${\bf F}=\left( {\bf F}.\hat{\bf e}_{\bf r} \right) \hat{\bf e}_{\bf r} +\left( {\bf F}.\hat{\bf e}_\theta \right) \hat{\bf e}_\theta +\left( {\bf F}.\hat{\bf e}_\phi \right) \hat{\bf e}_\phi$$ The balance is $$\begin{align} &{\bf F}.\hat{\bf e}_{\bf r}= - R \left( \cos^2\phi {\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2 + {\left( \frac{{\rm d}\phi}{{\rm d}t} \right)}^2 \right) \\ &{\bf F}.\hat{\bf e}_{\bf \theta}=R \left( \frac{{\rm d}}{{\rm d}t} \left( \cos\phi \frac{{\rm d}\theta}{{\rm d}t}\right) - \sin\phi \frac{{\rm d}\theta}{{\rm d}t}\frac{{\rm d}\phi}{{\rm d}t} \right)\\ &{\bf F}.\hat{\bf e}_\phi=R \left( \frac{{\rm d}^2\phi}{{\rm d}t^2} + \sin\phi \cos\phi {\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2 \right) \end{align}$$ We see "extra" terms in the equations $$ - R \left( \cos^2\phi {\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2 +{\left( \frac{{\rm d}\phi}{{\rm d}t} \right)}^2 \right) \hat{\bf e}_{\bf r} \qquad {\rm and}\qquad R \sin\phi \frac{{\rm d}\theta}{{\rm d}t} \left( - \frac{{\rm d}\phi}{{\rm d}t} \hat{\bf e}_{\bf \theta} +\cos\phi \frac{{\rm d}\theta}{{\rm d}t} \hat{\bf e}_{\bf \phi} \right).$$ Newton's law on the plane would just have the second time derivatives, so there are perceived "extra" forces. The first is called the centripetal force, and the scond the Coriolis force.
You should really check my algebra. This one uses the same definition of the transform, but our $\phi$ equations differ. This one gets the ${\left( \frac{{\rm d}\theta}{{\rm d}t} \right)}^2$ term in the $\phi$ equation like I do, but I suspect he measures $\phi$ down from the pole.