Invariant Manifolds

So a fixed point ${\bf F}({\bf u})$ is a zero dimensional invariant manifold. A periodic orbit, which is a closed curve in phase space $R^n$ is a one dimensional invariant manifold, and so on. The stable and unstable manifolds of fixed points and periodic orbits are maybe more interesting, and are important to understanding the global dynamics of the flow.
Invariant Manifolds are often defined in terms of transverse sections. A section is a $k-1$ dimensional manifold (possibly with a boundary) embedded in phase space $R^n$ which is transverse to the flow. That is, at every point on the section, the flow has some component which is not in the tangent space. Under the flow a point on the section moves away from the section.
One example is the Poincare section. As I defined it this is any point on a periodic orbit. The more common usage is a linear space orthogonal to the flow at the point. The flow takes the point back to itself after one period, and defines a mapping from a neighborhood of the point in the orthogonal subspace back to itself. A similar section exists for a quasiperiodic torus, but the section is a circle. The flow still maps the circle into itself. That is one use for transverse sections, they can be found as invariant sets of a map of dimension $n-1$ instead of an invariant set of a flow.
If the flow is restricted to an invariant manifolds the situation is that of a flow on a manifold, and if such a flow has a single transverse section it is called a global transverse section. Only certain flows on certain manifolds have a global transverse section. A quasiperiodic flow on a torus does, but Reeb flow on the same torus requires at least two sections. Basener describes flows on manifolds using flow box towers.
That's just a long way of justifying the definition. We will consider invariant manifolds which are the image of a $k-1$ dimensional manifold with boundary of initial conditions which under the flow defines a $k$ dimensional invariant manifold. For the stable and unstable manifolds of a fixed point, think of a sphere in the stable or unstable eigenspace with an arbitrarily small radius. For the stable and unstable manifolds of a periodic orbit a tube with arbitrarily small radius about the orbit in the subspace of the stable or unstable Floquet vectors.
The natural parameterization
The invariant set as defined is a manifold. An atlas for it can be built from the charts $\Omega_i({\bf s})$ defining the initial manifold $\Omega$. A local parameterization of the invariant manifold ${\bf u}_i({\bf s},t)$ defines a set of trajectories with $\Omega_i({\bf s})$ as as initial point, $$\begin{align} \frac{\partial}{\partial t} {\bf u}_i({\bf s},t)&={\bf F}({\bf u}_i({\bf s},t))\\ {\bf u}_i({\bf s},0)&=\Omega_i({\bf s}). \end{align}$$ If the initial manifold is dimension $k-1$ and the flow ${\bf F}$ is nowhere tangent to the initial set the invariant manifold is dimension $k$. The additional dimension is time.
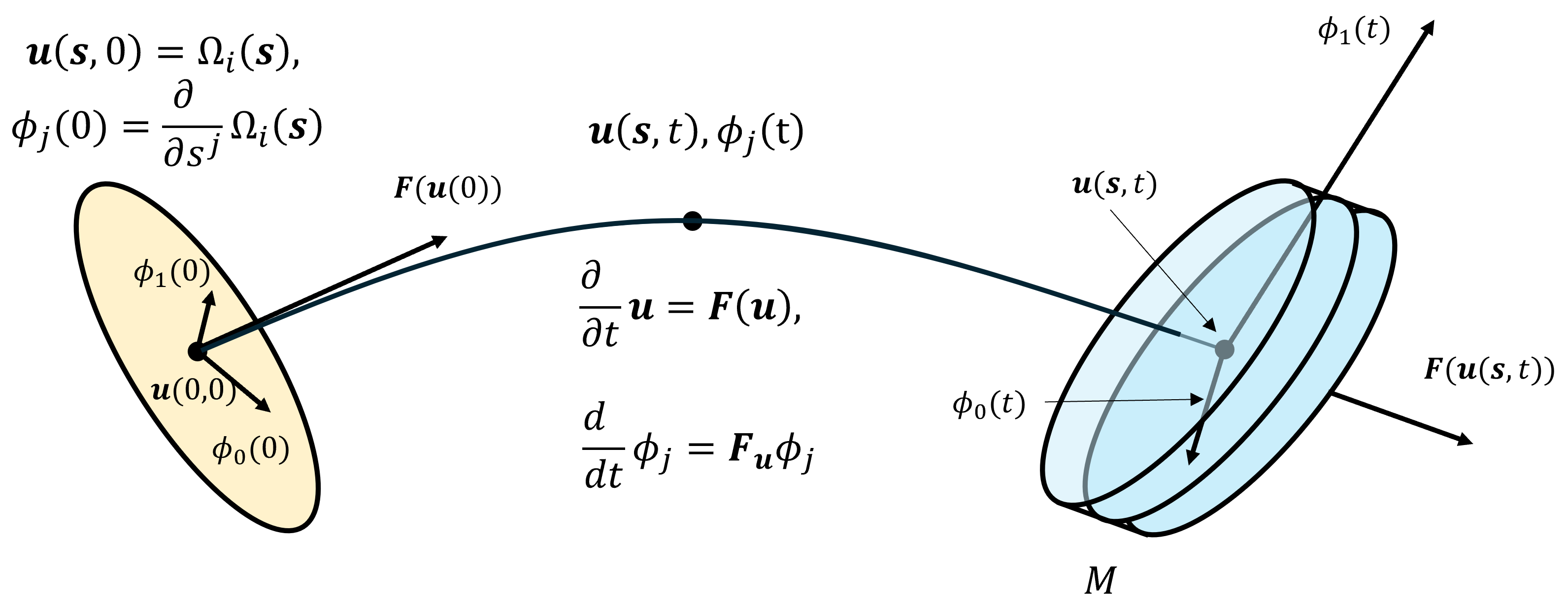
We're done, right? Maybe. Unfortunately for this local parameterization, many interesting flows have trajectories that either diverge or converge drastically (or both). That's just another way of saying that the parameterization is bad. But it does highlight that the difficulty in computing invariant manifolds is one of find a new parameterization. Otherwise the problem is just a matter of integrating trajectories. Spreading trajectories also means that a set of charts on the initial manifold will not cover the image of the initial manifold after some time.
Reparameterization: an orthonormal basis for the tangent space
We will fix the parameterization problem locally. Suppose we have a chart $i$ on the initial manifold $\Omega$ with the center of the chart ${\bf u}(0)=\Omega_i(0)$. The invariant manifold $M$ contains this point, and the $k-1$ tangents of the initial manifold and the flow vector ${\bf F}({\bf u}(0))$ span the tangent space of $M$. We can use the Gram-Schmidt algorithm to find a $k$ dimensional orthonormal basis $\Phi(0)$ for $M$.
As this tangent space evolves under the flow $\Phi' = {\bf F}_{\bf u}({\bf u}(t))\Phi$ it does not necessarily remain orthonormal, but we could re-orthogonalize at any point. Another approach is to use the idea of an inertial frame of reference, It us like taking very small steps along the trajectory, orthogonalizing and rotating the basis so that the basis remains orthogonal and parallel to the previous step. The modified basis evolves according to $$\frac{\partial u^i_{,j}}{\partial t} = F^i_{,p} u^p_{,j} - u^p_{,r} F^p_{,q} u^q_{,j}u^i_{,r}$$ (see [1]). Note that the linear operator in the second term isn't the usual matrix vector product. (If I was more familiar with coordinate free differential geometry there'd be a better way to write it.) In General Relativity the basis is called Riemannian Normal Coordinates. The subscripts with commas denote derivatives, so $F^i_{,j}$ is the Jacobian, and for fixed $j$ $u^i_{,j}$ is the $i^{\rm th}$ coordinate of the $j^{\rm th}$ basis vector. The second term lies in the span of the basis, and it is easy to show that the basis remains orthonormal. The Jacobians are evaluated at ${\bf u}(t)$. A similar more complicated system, can be written for the curvature and higher derivatives.

Given a trajectory on $M$, an orthonormal basis for the tangent space of $\Omega$ at the origin of a chart and the flow vector at that point can be used as an initial condition that can be integrated along the trajectory to find an orthonormal basis for the tangent space of $M$ at points ${\bf u}(t)$. The curvature can be found in a similar way, and the chart radius estimated.
The chart mapping
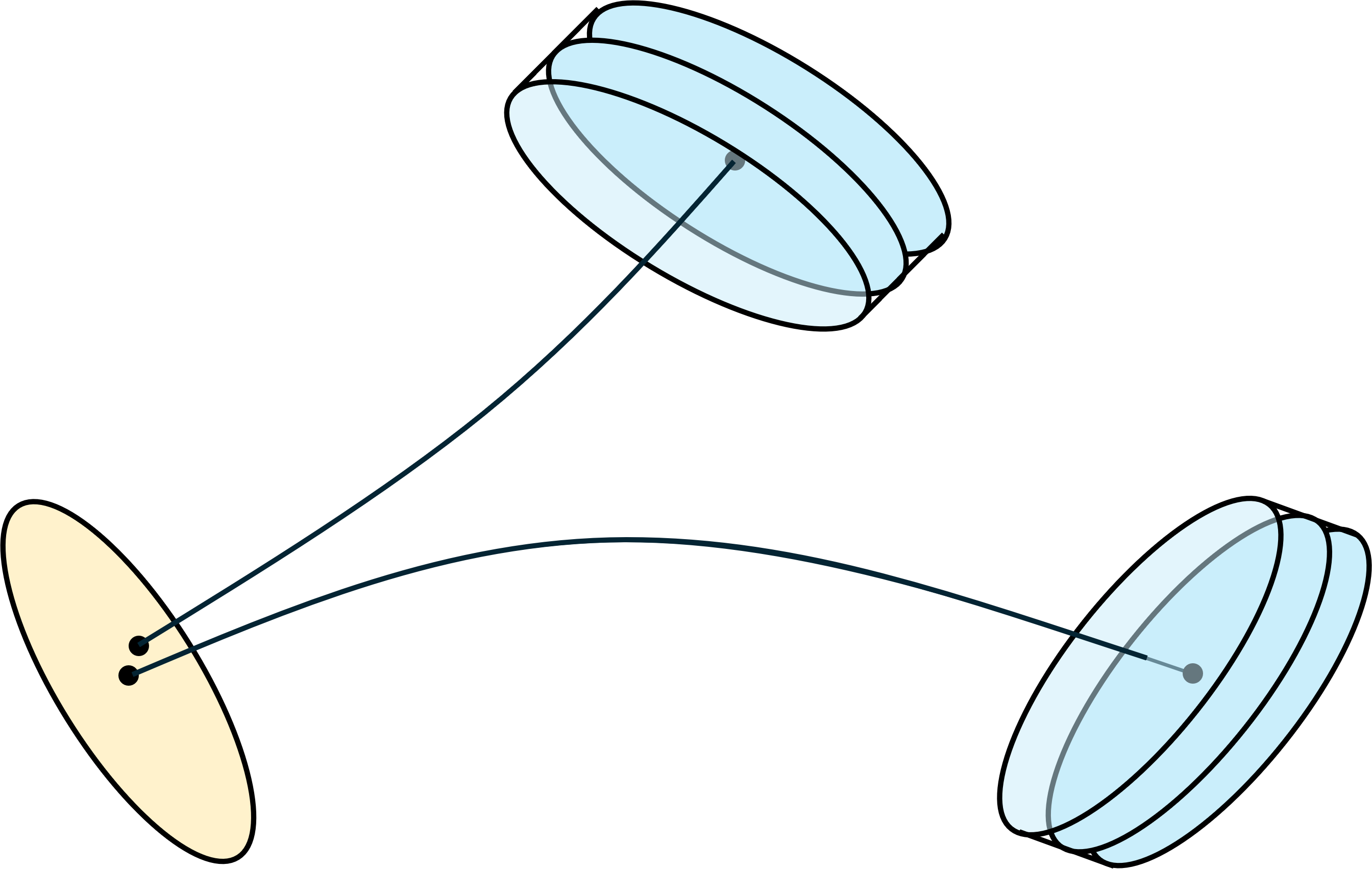
Because trajectories spread the image of an initial set of charts probably will not cover $M$. If a continuation method is used to find a covering we must be able to project a point in the tangent space of $M$ onto $M$. Given a chart with center ${\bf u}_i(0,\tau)$ on an invariant manifold $M$ (the image of the center of chart $i$ on the initial manifold $\Omega$ after time $\tau$), we can project a point ${\bf s}$ onto $M$ by solving the TPBVP $$\begin{align} &{\bf u}'=T {\bf F}({\bf u})\\ &{\bf u}(0)=\Omega_i(\sigma)\\ &\Phi^* ( {\bf u}(1) - ( {\bf u}_i(0,\tau) + \Phi {\bf s})) = 0\\ \end{align}$$ The new point is ${\bf u}_i({\bf s},\tau({\bf s}))={\bf u}(1)$ with $\tau({\bf s})=T$. I hope that notation is clear. This is a system of $n$ ODE's with $n+k$ boundary conditions with extra variables $T\in R$ and $\sigma\in R^{k-1}$.

To find the tangents at this new point, first find an orthonormal basis for the space spanned by the tangents $\partial \Omega_i (\sigma) / \partial \sigma^j$ and the flow ${\bf F}({\bf u}(0))$, and integrate it forward time $T$ using the equations for propagating the inertial frame.
In [1] we proposed integrating the chart on the initial manifold forward in time with the orthonormal basis. This was called a fattened trajectory. This leaves gaps where trajectories spread, and an interpolation was used when chart domains separated. The approach described here requires that trajectories ${\bf u}(t)$ connecting back to the initial manifold be saved at each point on the computed invariant manifold. The trajectories can be discarded when the charts no longer overlap new charts on the boundary, but that still is extra storage. This approach avoids the interpolation, which we found to be unreliable, at the expense of this extra storage.
Since the stored trajectory connecting the center of a chart to the initial set is only used to project new points, and the only points projected by the continuation algorithm are near the boundary, only the points on the boundary list need to store the extra information. For the others, unless needed for other purposes, only the center and tangents are needed (interior charts can overlap bew charts added at the boundary).
Note that ${\bf u}(0)$ may not lie in the domain of the chart on the initial manifold. If an iterative solver is used and $\sigma$ moves out of the chart domain the system would need to be modified to use an adjacent chart.
Stable and Unstable Manifold of Hyperbolic Fixed Points
The existance and stability of stable and unstable manifolds associated with hyperbolic fixed points (the Hartmann-Grubmann theorem) is one the most important results in dynamical systems. It says that near a hyperbolic fixed points (where the eigenvalues of the Jacobian of the flow splits into seperate positive (unstable) and negative (stable) parts, there are invariant manifolds associated with each part, tangent to the space spanned by the associated eigenvectors which are stable to perturbations of the flow. Points on the stable manifold approach the fixed point, and those on the unstable manifold move away. Points are attracted to the unstable manifold (I know, that sounds backwards), and repelled by the stable manifold.
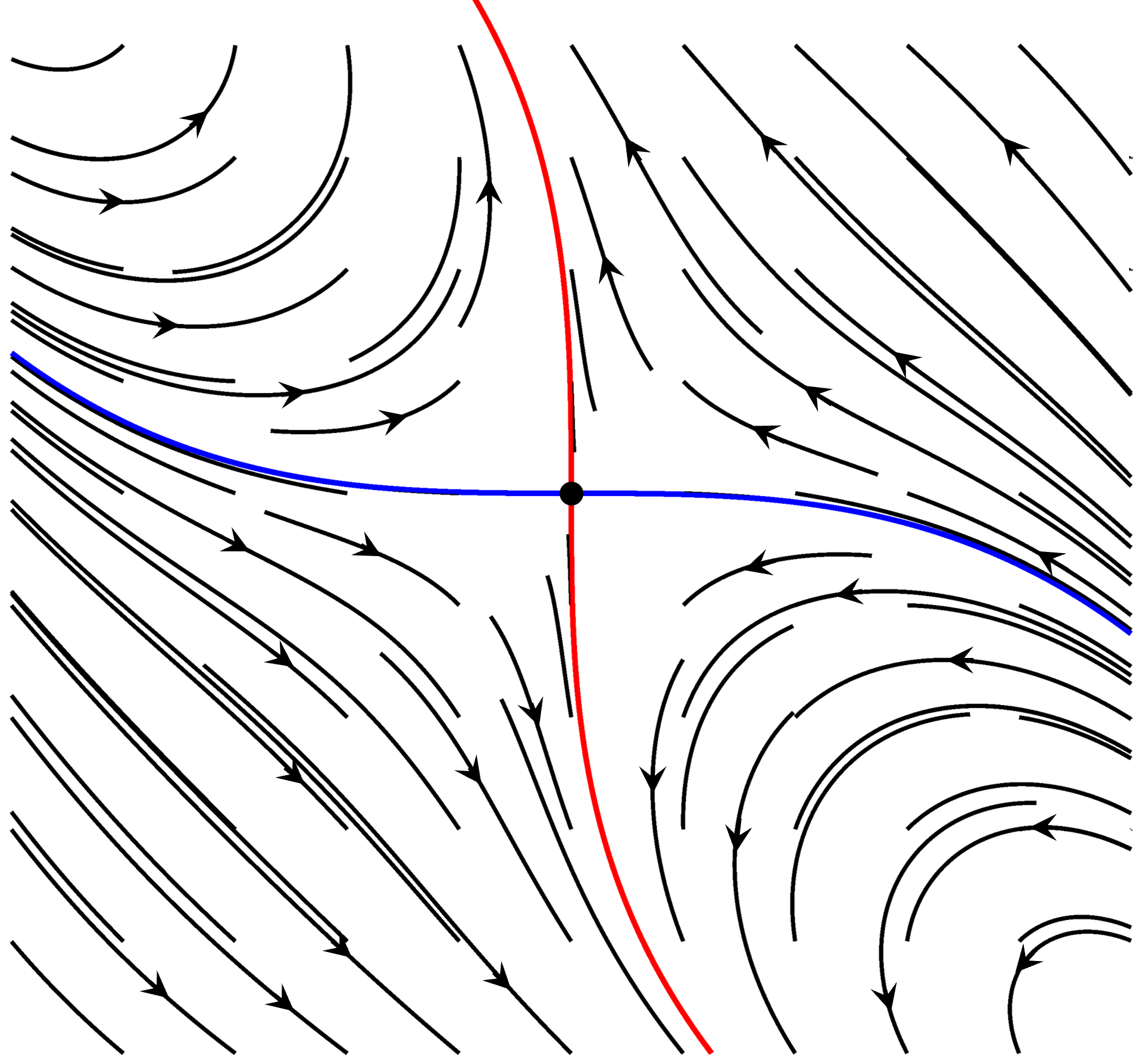
At first glance this seems like a different thing than we discussed above. There is an initial set (the fixed point), but the flow is zero on it, not transverse to it. The usual approach is to take a small ball in the eigenspace, centered at the fixed point. Since the manifold is tangent to the eigenspace, this serves as a special chart. Points on the ball are near the manifold. Integrating them forward for the unstable manifold and backward for the stable manifold, near the fixed point the manifolds are attracting, and small errors are damped out. Further away from the fixed point this isn't necessarily true, but with a small enough ball, the surface of the balls serves as an initial set.
Higher order approximations can be found. The basic equation is $$ {\bf F}({\bf u}({\bf s})) = {\bf u}_{\bf s} ({\bf s}) . {\bf a}({\bf s}).$$ This just says that at any point on the manifold there is a direction in the tangent space which is parallel to the flow. (The flow is tangent to the manifold.) The function ${\bf a}({\bf s})$ gives the flow on the invariant manifold in the tangent coordinates. It can be eliminated $$ {\bf a}({\bf s}) = {\bf u}_{\bf s}({\bf s})^T {\bf F}({\bf u}({\bf s}))$$ which leaves $$(I - {\bf u}_{\bf s}({\bf s}) {\bf u}_{\bf s}({\bf s})^T) {\bf F}({\bf u}({\bf s})) = 0.$$
There is freedom here in the parameterization. If we adopt a locally Euclidean parameterization, we have $${\bf u}_{\bf s}({\bf s})^T {\bf u}_{\bf s}({\bf s}) = I.$$ These two equations hold at any point on the manifol, so we can differentiate and get equations for the derivatives of the o.n. basis for the tangent space ${\bf u}_{\bf s}$ as a function of ${\bf s}$. $$\begin{align} & (I - {\bf u}_{\bf s} {\bf u}_{\bf s}^T) {\bf F}_{\bf u}{\bf u}_{\bf s} - \left( {\bf u}_{\bf s} {\bf u}_{\bf ss}^T + {\bf u}_{\bf ss} {\bf u}_{\bf s}^T \right) {\bf F} = 0\\ & (I - {\bf u}_{\bf s} {\bf u}_{\bf s}^T) \left( {\bf F}_{\bf u}{\bf u}_{\bf ss} + {\bf F}_{\bf uu}{\bf u}_{\bf s}{\bf u}_{\bf s} \right) -\left( {\bf u}_{\bf ss} {\bf u}_{\bf s}^T + {\bf u}_{\bf s}{\bf u}_{\bf ss}^T \right){\bf F}_{\bf u}{\bf u}_{\bf s} -\left( {\bf u}_{\bf sss} {\bf u}_{\bf s}^T + 2 {\bf u}_{\bf ss} {\bf u}_{\bf ss}^T + {\bf u}_{\bf s}^T {\bf u}_{\bf sss}^T \right) {\bf F} = 0 \end{align}$$ $$\begin{align} & {\bf u}_{\bf s}^T {\bf u}_{\bf s} = I\\ & {\bf u}_{\bf s}^T {\bf u}_{\bf ss} = 0 \end{align}$$ This looks like a mess, but at ${\bf s}=0$ we have ${\bf u}(0)={\bf u}_0$ and ${\bf F}({\bf u}_0)=0$. We also require that ${\bf u}^0_{\bf s}$ be an o.n. basis for an invariant subspace of ${\bf F}^0_{\bf u}$, which means there is a $k\times k$ matrix $\Lambda$ so that ${\bf F}^0_{\bf u}{\bf u}^0_{\bf s}={\bf u}^0_{\bf s}\Lambda$ with ${({\bf u}^0_{\bf s})}^T {\bf u}^0_{\bf s} = I$. Therefore, at ${\bf s} = 0$ $$\begin{align} & (I - {\bf u}^0_{\bf s} {({\bf u}^0_{\bf s})}^T) {\bf u}^0_{\bf s}\Lambda = 0 \\ \\ & (I - {\bf u}^0_{\bf s} {({\bf u}^0_{\bf s})}^T) {\bf F}^0_{\bf u}{\bf u}^0_{\bf ss} - {\bf u}^0_{\bf ss} \Lambda = - (I - {\bf u}^0_{\bf s} {({\bf u}^0_{\bf s})}^T) {\bf F}^0_{\bf uu}{\bf u}^0_{\bf s}{\bf u}^0_{\bf s} \end{align}$$ $$\begin{align} & {({\bf u}^0_{\bf s})}^T {\bf u}^0_{\bf ss} = 0 \end{align}$$ The first is identically zero and the second and third are a linear system for ${\bf u}^0_{\bf ss}$. The second has a right null space which is the invariant subspace, and the third removes this degeneracy. If this system is nonsingular the implicit function theorem gives the existance of ${\bf u}({\bf s})$ for a neighborhood of the origin.
The linear system is not squarte, with a left null space spanned by $ {({\bf u}^0_{\bf s})}^T$. An equivalent square system can be found by adding an auxilliary vector $\xi$ of length $k$ and solve the equivalent system $$\begin{align} & (I - {\bf u}^0_{\bf s} {({\bf u}^0_{\bf s})}^T) {\bf F}^0_{\bf u}{\bf u}^0_{\bf ss} - {\bf u}^0_{\bf ss} \Lambda + {\bf u}^0_{\bf s}\xi = - (I - {\bf u}^0_{\bf s} {({\bf u}^0_{\bf s})}^T) {\bf F}^0_{\bf uu}{\bf u}^0_{\bf s}{\bf u}^0_{\bf s} \\ & {({\bf u}^0_{\bf s})}^T {\bf u}^0_{\bf ss} = 0 \end{align}$$ which is a square system with a solution $\xi=0$.
To find systems for the higher derivatives, I'd let $$P=I - {\bf u}_{\bf s} {\bf u}_{\bf s}^T$$ and write the basis equation as $PF=0$. Derivatives of $P$ and $F$ (a composition of functions) can then be found. $$\begin{align} P & = I - {\bf u}_{\bf s} {\bf u}_{\bf s}^T \\ - P_{\bf s} & = {\bf u}_{\bf ss} {\bf u}_{\bf s}^T + {\bf u}_{\bf s}{\bf u}_{\bf ss}^T \\ - P_{\bf ss} &= {\bf u}_{\bf sss} {\bf u}_{\bf s}^T + 2 {\bf u}_{\bf ss} {\bf u}_{\bf ss}^T + {\bf u}_{\bf s} {\bf u}_{\bf sss}^T \\ - P_{\bf sss} &= {\bf u}_{\bf ssss} {\bf u}_{\bf s}^T + 3 {\bf u}_{\bf sss} {\bf u}_{\bf ss}^T + 3 {\bf u}_{\bf ss}^T {\bf u}_{\bf sss}^T + {\bf u}_{\bf s} {\bf u}_{\bf ssss}^T \\ \end{align}$$ This obviously has coeeficients from Pascal's triangle. The derivatives of the composition are not as obviously generated, with $$\begin{align} F_{\bf s} & = {\bf F}_{\bf s} {\bf u}_{\bf s} \\ F_{\bf ss} &= {\bf F}_{\bf u}{\bf u}_{\bf ss} + {\bf F}_{\bf uu}{\bf u}_{\bf s}{\bf u}_{\bf s} \\ F_{\bf sss} &= {\bf F}_{\bf u}{\bf u}_{\bf sss} + 3 {\bf F}_{\bf uu}{\bf u}_{\bf s}{\bf u}_{\bf ss} + {\bf F}_{\bf uuu}{\bf u}_{\bf s}{\bf u}_{\bf s}{\bf u}_{\bf s} \\ \end{align}$$ And the systems for the derivatives of ${\bf u}({\bf s})$ are $$\begin{align} & PF=0 \\ & P F_{\bf s} + P_{\bf s} F=0 \\ & P F_{\bf ss} + 2 P_{\bf s} F_{\bf s} + P_{\bf ss} F =0 \\ & P F_{\bf sss} + 3 P_{\bf s} F_{\bf ss} + 3 P_{\bf ss} F_{\bf s} + P_{\bf sss} F =0 \\ \end{align}$$ There's another Pascal triangle here. The leading coefficients come from the product of $P$ and the first term in the $m^{\rm th}$ derivative of ${\bf F}$ (${\bf F}_{\bf u}$ operating on the $m^{th}$ derivative of ${\bf u}$) minus $m$ times the first term of the $(m-1)^{\rm th}$ derivative of $P$ (sum of the $m^{\rm th}$ derivative of ${\bf u}$ times ${\bf u}_{\bf s}^T$ and the transpose) with $F_{\bf s}={\bf u}_{\bf s}\Lambda$.
The system for the third derivative at the origin is $$ P {\bf F}_{\bf u}{\bf u}_{\bf sss} + 3 P {\bf F}_{\bf uu}{\bf u}_{\bf s}{\bf u}_{\bf ss} + P {\bf F}_{\bf uuu}{\bf u}_{\bf s}{\bf u}_{\bf s}{\bf u}_{\bf s} - 3 \left( {\bf u}_{\bf ss} {\bf u}_{\bf s}^T + {\bf u}_{\bf s}{\bf u}_{\bf ss}^T \right) \left( {\bf F}_{\bf u}{\bf u}_{\bf ss} + {\bf F}_{\bf uu}{\bf u}_{\bf s}{\bf u}_{\bf s} \right) -{\bf F}_{\bf s} {\bf u}_{\bf s} 3 \left( {\bf u}_{\bf sss} {\bf u}_{\bf s}^T + 2 {\bf u}_{\bf ss} {\bf u}_{\bf ss}^T + {\bf u}_{\bf s} {\bf u}_{\bf sss}^T \right) {\bf F}_{\bf s} {\bf u}_{\bf s} $$
[1] Michael E. Henderson, "Computing Invariant Manifolds by Integrating Fat Trajectories", SIAM J. Appl. Dyn. Sys., 4(4), pp. 832-882, 2005.
[2] William Basener, "Every nonsingular C1 flow on a closed manifold of dimension greater than two has a global transverse disk", Topology and its Applications 135(1-3), pp. 131-148, 2004.