Representing and manipulating finite convex polyhedra in any dimension
We have finite convex polyhedra represented as a set of inequalities representing half spaces $$\begin{matrix} i : & {\bf u}.{\bf n}_i \leq o_i \end{matrix}$$ Each defining half space has an index $i$ with $i\in[0,N)$. I've written this with the center as the origin. With this representation subtracting a half space is just a matter of adding the new half space to the list. There are some subtleties with half spaces becoming redundant, but to test a point for being in the polyhedra that doesn't matter.
Another way to represent the polyhedron is as a convex combination of vertices $$\begin{align} & {\bf u}\in P \longrightarrow {\bf u} = \sum \alpha_i {\bf v}_i,\\ \\ & 0\leq\alpha_i\leq 1 \qquad\qquad\sum \alpha =1. \end{align}$$ This makes generating points in the polyhedra simple, they have all $\alpha$'s except one zero. Edges have exactly two non-zero $\alpha$'s, and so on for faces of higher dimension.
To subtract a half space from this second representation we will use the algorithm described in [1].
First add an index to each vertex which is the set of defining inequalities which are equalities. For a $k$ dimensional polyhedron there must be at least $k+1$ equalities. The index can be used to label higher dimensional faces. Edges will have $k$ indices, two dimensional faces $k-1$ and in general an $m$ dimensional faces will have $k-m$ indices. A vertex will lie on an face if the face indices are in the index set of the vertex. To determine if a set of vertices lies on the same face we take the intersection of all of the index sets of the vertices. If the vertices have $k-m$ indices in common they lie on an $m$ dimensional face and the common indices are the index set of the face. Each index is an $k-1$ dimensional faces containing the $m$ dimensional face.
Example
As an example, consider the four dimensional cube containing a ball of radius $R$ at the origin $$\left\{ \begin{array}{rlr} 0: & {\bf u}.\hat{\bf e}_0 \geq & -1.2 R \\ 1: & {\bf u}.\hat{\bf e}_0 \leq & 1.2 R \\ 2: & {\bf u}.\hat{\bf e}_1 \geq & -1.2 R \\ 3: & {\bf u}.\hat{\bf e}_1 \leq & 1.2 R \\ 4: & {\bf u}.\hat{\bf e}_2 \geq & -1.2 R \\ 5: & {\bf u}.\hat{\bf e}_2 \leq & 1.2 R \\ 6: & {\bf u}.\hat{\bf e}_3 \geq & -1.2 R \\ 7: & {\bf u}.\hat{\bf e}_3 \leq & 1.2 R \\ \end{array} \right.$$ This has the sixteen vertices $$\left\{ \begin{array}{rll} 0: & 1.2 R (\phantom{-}1,\phantom{-}1,\phantom{-}1,\phantom{-}1) & [0,2,4,6] \\ 1: & 1.2 R (-1,\phantom{-}1,\phantom{-}1,\phantom{-}1) & [1,2,4,6] \\ 2: & 1.2 R (\phantom{-}1,-1,\phantom{-}1,\phantom{-}1) & [0,3,4,6] \\ 3: & 1.2 R (-1,-1,\phantom{-}1,\phantom{-}1) & [1,3,4,6] \\ 4: & 1.2 R (\phantom{-}1,\phantom{-}1,-1,\phantom{-}1) & [0,2,5,6] \\ 5: & 1.2 R (-1,\phantom{-}1,-1,\phantom{-}1) & [1,2,5,6] \\ 6: & 1.2 R (\phantom{-}1,-1,-1,\phantom{-}1) & [0,3,5,6] \\ 7: & 1.2 R (-1,-1,-1,\phantom{-}1) & [1,3,5,6] \\ 8: & 1.2 R (\phantom{-}1,\phantom{-}1,\phantom{-}1,-1) & [0,2,4,7] \\ 9: & 1.2 R (-1,\phantom{-}1,\phantom{-}1,-1) & [1,2,4,7] \\ 10: & 1.2 R (\phantom{-}1,-1,\phantom{-}1,-1) & [0,3,4,7] \\ 11: & 1.2 R (-1,-1,\phantom{-}1,-1) & [1,3,4,7] \\ 12: & 1.2 R (\phantom{-}1,\phantom{-}1,-1,-1) & [0,2,5,7] \\ 13: & 1.2 R (-1,\phantom{-}1,-1,-1) & [1,2,5,7] \\ 14: & 1.2 R (\phantom{-}1,-1,-1,-1) & [0,3,5,7] \\ 15: & 1.2 R (-1,-1,-1,-1) & [1,3,5,7] \\ \end{array} \right.$$ A general cube will have vertices with $\pm1$ in coordinate $i$, with an index $2^i$ is the sign is positive and $2^i+1$ if it is negative.
Given the half spaces the vertices can be found, but it requires taking all combinations of $k$ of them, finding if they have a point in common, and then checking the remaining inequaties to see if they are satisfied. The index of the vertex is the set of exactly satisfied inequalities, and of course if any are violated the common point is not a vertex. If there are $N$ half spaces, this requires $N!/(N-k)!$ solutions of $k\times k$ linear systems. For simplices every choice of $k$ half spaces corresponds to a vertex, and for cube the $2^k$ vertices correspond to a labeling of the half spaces by a $k$ digit binary number with 0 if the half space is to the left of that coordinate axis and 1 if to the right. Each binary number generates a vertex.
Subtracting a half space
Subtracting a half space removes vertices that lie outside the half space and adds vertices on edges which have one vertex inside the half space and the other out. A simple algorithm is the mark the vertices with being interior or exterior, then add a vertex for each vertex pair with $k$ indices in common. Finally the vertices marked exterior can be deleted. If there are $M$ vertices. the step of testing edges requires $M(M-1)$ tests. This can be reduced by storing the edges (this is what [1] suggests). This way only the existing edges need to be tested, but it does require that new edges be found by testing pairs of the new vertices.
Example
Consider a three dimensional cube (because we can draw it), defined six half spaces $$Half~spaces~\left\{ \begin{array}{rlr} 0: & {\bf u}.\hat{\bf e}_0 \geq & -1 \\ 1: & {\bf u}.\hat{\bf e}_0 \leq & 1 \\ 2: & {\bf u}.\hat{\bf e}_1 \geq & -1 \\ 3: & {\bf u}.\hat{\bf e}_1 \leq & 1 \\ 4: & {\bf u}.\hat{\bf e}_2 \geq & -1 \\ 5: & {\bf u}.\hat{\bf e}_2 \leq & 1 \\ \end{array} \right.$$ This has eight vertices and twelve edges $$$$Vertices~\left\{ \begin{array}{rll} 0: & (\phantom{-}1,\phantom{-}1,\phantom{-}1) & [0,2,4] \\ 1: & (-1,\phantom{-}1,\phantom{-}1) & [1,2,4] \\ 2: & (\phantom{-}1,-1,\phantom{-}1) & [0,3,4] \\ 3: & (-1,-1,\phantom{-}1) & [1,3,4] \\ 4: & (\phantom{-}1,\phantom{-}1,-1) & [0,2,5] \\ 5: & (-1,\phantom{-}1,-1) & [1,2,5] \\ 6: & (\phantom{-}1,-1,-1) & [0,3,5] \\ 7: & (-1,-1,-1) & [1,3,5] \\ \end{array} \right.$$ $$Edges~\left\{ \begin{array}{rll} 0: & (0,1) & [2,4] \\ 1: & (0,2) & [0,4] \\ 2: & (0,4) & [0,2] \\ 3: & (1,3) & [1,4] \\ 4: & (1,5) & [1,2] \\ 5: & (2,3) & [3,4] \\ 6: & (2,6) & [0,3] \\ 7: & (3,7) & [1,3] \\ 8: & (4,5) & [2,5] \\ 9: & (4,6) & [0,5] \\ 10: & (5,7) & [1,5] \\ 11: & (6,7) & [3,5] \\ \end{array} \right.$$
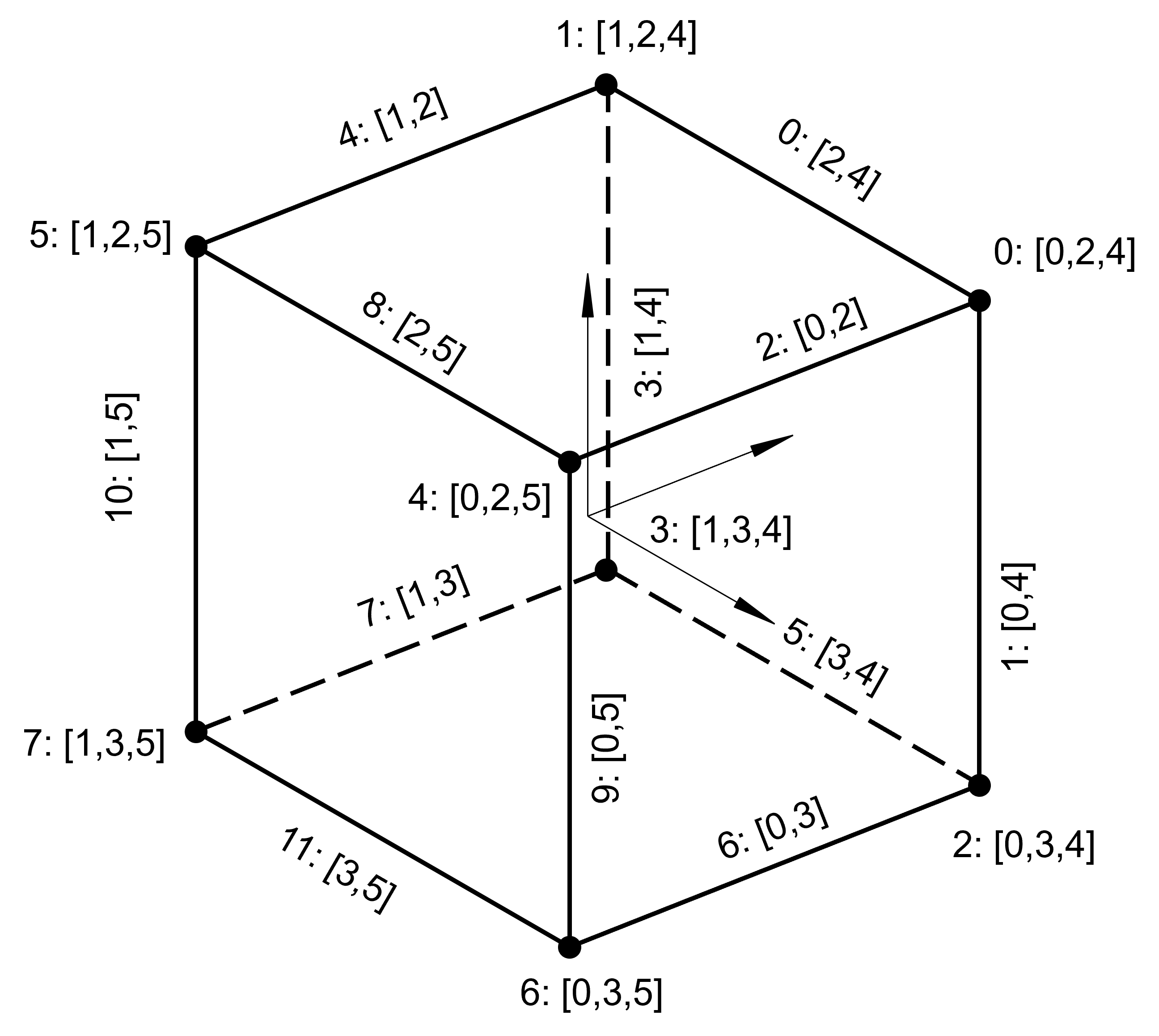
You can see that edge 7 has endpoints 3 and 7 with index sets $[1,3,4]$ and $[1,3,5]$. The intersection of these two sets is $[1,3]$ it has $k-1=2$ indices so is an edge, and the edge has index set $[1,3]$.
Now suppose we remove a half space $$ {\bf u}.(.7,.7,.14)\gt .5$$ we have $$Vertices~\left\{ \begin{array}{rl} \color{red}{0: }& \color{red}{(\phantom{-}1,\phantom{-}1,\phantom{-}1).(.7,.7,.14)=1.54\gt .5} \\ 1: & (-1,\phantom{-}1,\phantom{-}1).(.7,.7,.14)=0.14\lt .5 \\ 2: & (\phantom{-}1,-1,\phantom{-}1).(.7,.7,.14)=0.14\lt .5 \\ 3: & (-1,-1,\phantom{-}1).(.7,.7,.14)=-1.26\lt .5 \\ \color{red}{4:}& \color{red}{(\phantom{-}1,\phantom{-}1,-1).(.7,.7,.14)=1.26\gt .5}\\ 5: & (-1,\phantom{-}1,-1).(.7,.7,.14)= 0.14 \lt .5 \\ 6: & (\phantom{-}1,-1,-1).(.7,.7,.14)=-0.14 \lt .5 \\ 7: & (-1,-1,-1).(.7,.7,.14)=-1.54 \lt .5 \\ \end{array} \right.$$ $$Edges~\left\{ \begin{array}{rll} \color{blue}{0:} & \color{blue}{(0,1)} & \color{blue}{[2,4]} \\ \color{blue}{1:} & \color{blue}{(0,2)} & \color{blue}{[0,4]} \\ \color{red}{2:} & \color{red}{(0,4)} & \color{red}{[0,2]} \\ 3: & (1,3) & [1,4] \\ 4: & (1,5) & [1,2] \\ 5: & (2,3) & [3,4] \\ 6: & (2,6) & [0,3] \\ 7: & (3,7) & [1,3] \\ \color{blue}{8:} & \color{blue}{(4,5)} & \color{blue}{[2,5]} \\ \color{blue}{9:} & \color{blue}{(4,6)} & \color{blue}{[0,5]} \\ 10: & (5,7) & [1,5] \\ 11: & (6,7) & [3,5] \\ \end{array} \right.$$ so vertices 0 and 4 (red) lie on the "wrong" side of the plane and will not be present in the updated polyhedron. Edges 0, 1, and 2 have vertex 0 as an endpoint and edges 2, 8, and 9 have vertex 4. So edges 0, 1, 8, and 9 (blue) will need to be shortened and new vertices added and edge 2 (red) will be removed.
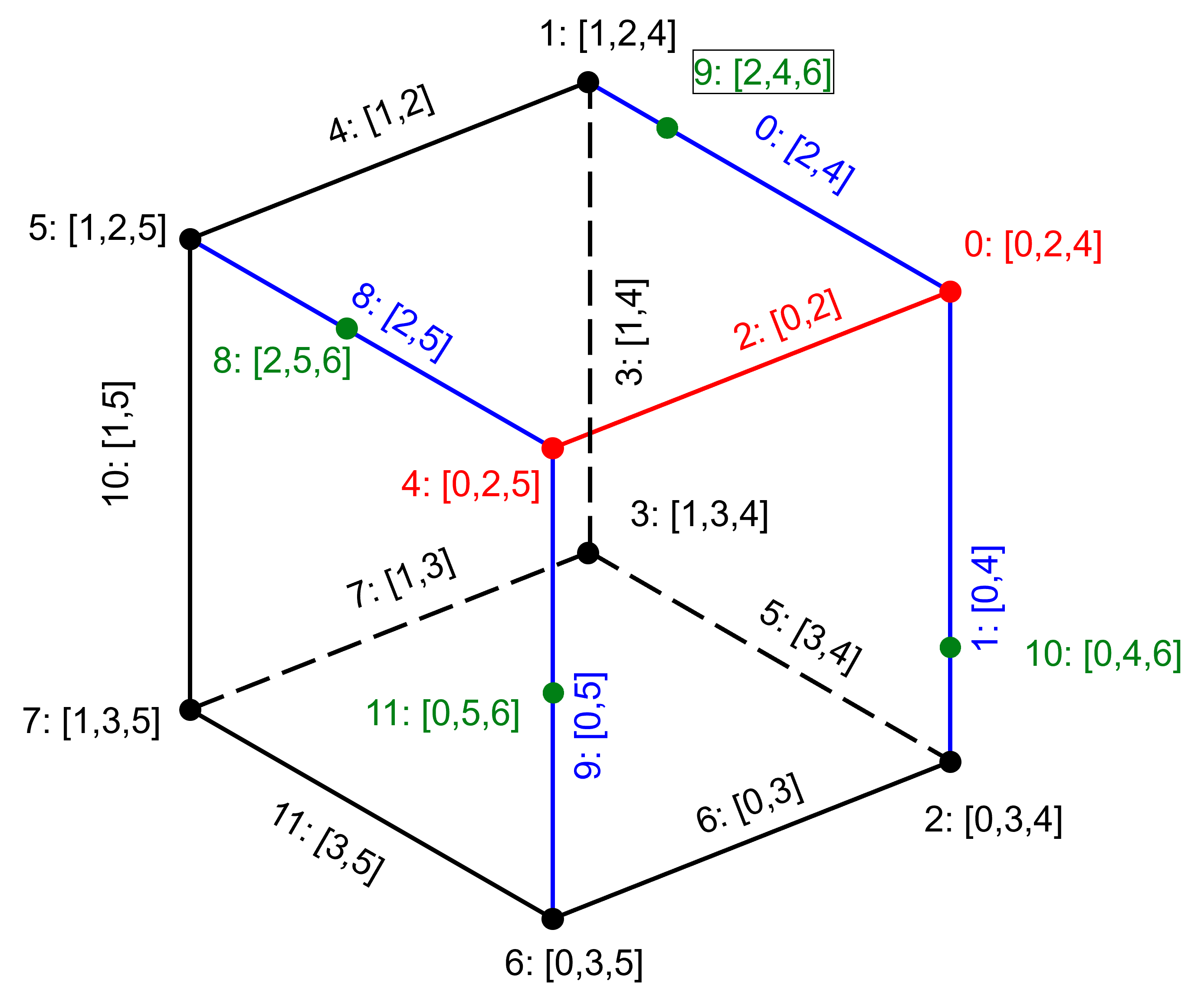
The vertices added on the shortened edges will have the index of the new half space (6) added to their index sets. The coordinates of the vertices are found by finding where a convex combination of the two endpoints crosses the plane defining the new half space. For edge 8 that means finding $0\leq t\leq 1$ so that $$\begin{align} & ((1-t)(1,1,-1) +t (-1,1,-1) ).(.7,.7,.14)=.5\\ & {\rm or} \qquad t=0.54 \end{{align}$$ The new vertex (8) is then $(1-t)(1,1,-1) +t (-1,1,-1)=(-0.09,1,-1)$ and will have index set $[2,5,6]$. Edge 8 keeps the same index set, but the endpoints change from $(4,5)$ to $(5,8)$. Repeating this for edges 0, 1 and 9 gives new vertices (green) 9, 10, and 11 $$Vertices~\left\{ \begin{array}{rll} \color{red}{0:} & \color{red}{(\phantom{-}1,\phantom{-}1,\phantom{-}1)} & \color{red}{[0,2,4]} \\ 1: & (-1,\phantom{-}1,\phantom{-}1) & [1,2,4] \\ 2: & (\phantom{-}1,-1,\phantom{-}1) & [0,3,4] \\ 3: & (-1,-1,\phantom{-}1) & [1,3,4] \\ \color{red}{4:} & \color{red}{(\phantom{-}1,\phantom{-}1,-1)} & \color{red}{[0,2,5]} \\ 5: & (-1,\phantom{-}1,-1) & [1,2,5] \\ 6: & (\phantom{-}1,-1,-1) & [0,3,5] \\ 7: & (-1,-1,-1) & [1,3,5] \\ \color{green}{8:} & \color{green}{(-0.09,1,-1)} & \color{green}{[2,5,6]} \\ \color{green}{9:} & \color{green}{(-0.49,1,1)} & \color{green}{[2,4,6]} \\ \color{green}{10:} & \color{green}{(1,-0.49,1)} & \color{green}{[0,4,6]} \\ \color{green}{11:} & \color{green}{(1,-0.09,-1)} & \color{green}{[0,5,6]} \\ \end{array} \right.$$ $$Edges~\left\{ \begin{array}{rll} \color{blue}{0:} & \color{blue}{(0,9)} & \color{blue}{[2,4]} \\ \color{blue}{1:} & \color{blue}{(0,10)} & \color{blue}{[0,4]} \\ \color{red}{2:} & \color{red}{(0,4)} & \color{red}{[0,2]} \\ 3: & (1,3) & [1,4] \\ 4: & (1,5) & [1,2] \\ 5: & (2,3) & [3,4] \\ 6: & (2,6) & [0,3] \\ 7: & (3,7) & [1,3] \\ \color{blue}{8:} & \color{blue}{(4,8)} & \color{blue}{[2,5]} \\ \color{blue}{9:} & \color{blue}{(4,11)} & \color{blue}{[0,5]} \\ 10: & (5,7) & [1,5] \\ 11: & (6,7) & [3,5] \\ \color{green}{12:} & \color{green}{(8,9)} & \color{green}{[2,6]} \\ \color{green}{13:} & \color{green}{(9,10)} & \color{green}{[4,6]} \\ \color{green}{14:} & \color{green}{(10,11)} & \color{green}{[0,6]} \\ \color{green}{15:} & \color{green}{(8,11)} & \color{green}{[5,6]} \\ \end{array} \right.$$ The final step is to check the new vertices for edges connecting them. If the intersection of the index sets of two new vertices has exactly $k-1=2$ members an edge must be added connecting the pair of vertices with index set which is the intersection of the index sets. For example, vertices 8 and 9 share indices 2 and 6, so a new edge 12 (green) with end points $(8,9)$ and index set $[2,6]$ is created. For this example there are three other new edges. Oh, and throw away the red things.
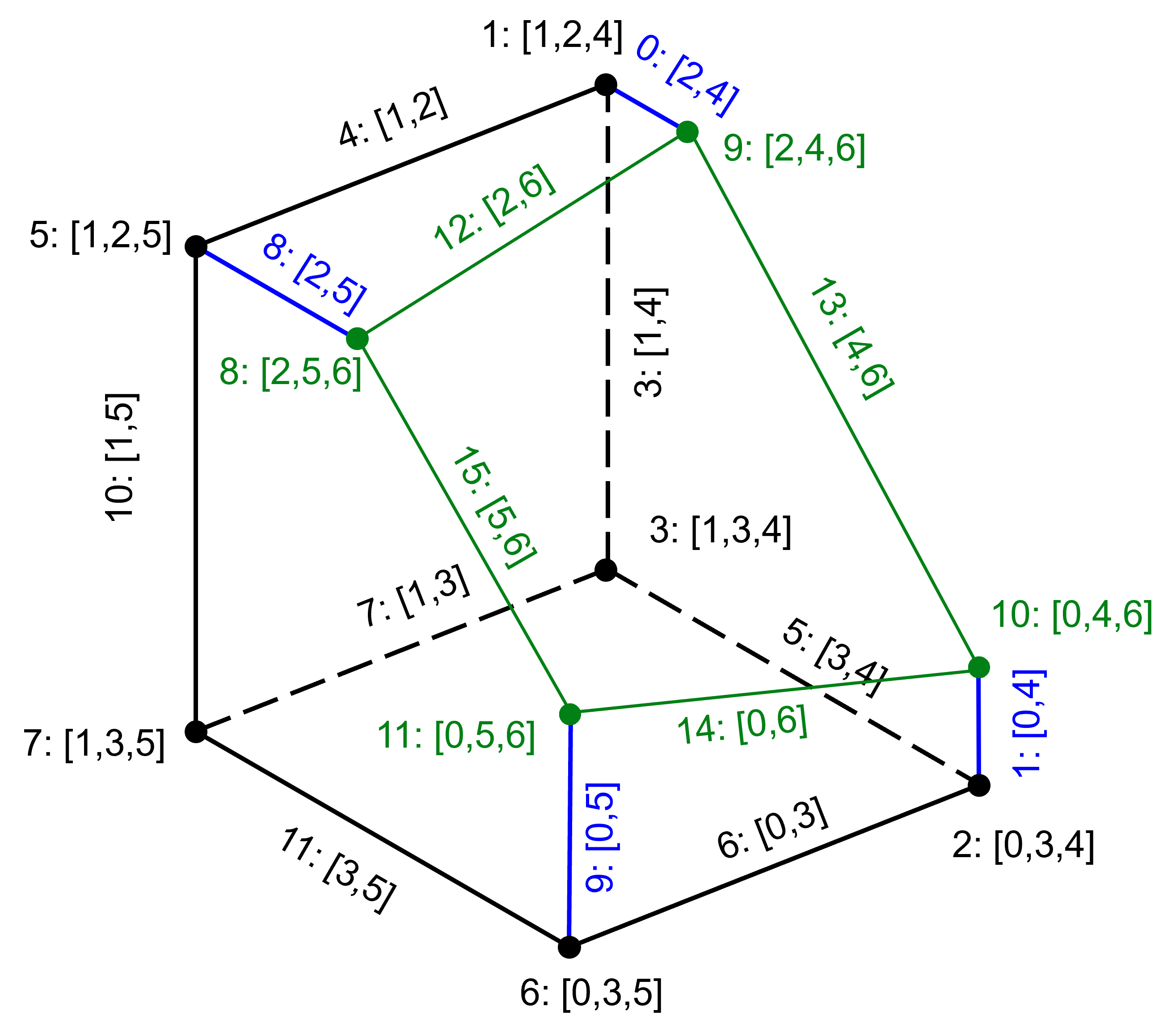
$$Vertices~\left\{ \begin{array}{rll} 1: & (-1,\phantom{-}1,\phantom{-}1) & [1,2,4] \\ 2: & (\phantom{-}1,-1,\phantom{-}1) & [0,3,4] \\ 3: & (-1,-1,\phantom{-}1) & [1,3,4] \\ 5: & (-1,\phantom{-}1,-1) & [1,2,5] \\ 6: & (\phantom{-}1,-1,-1) & [0,3,5] \\ 7: & (-1,-1,-1) & [1,3,5] \\ \color{green}{8:} & \color{green}{(-0.09,1,-1)} & \color{green}{[2,5,6]} \\ \color{green}{9:} & \color{green}{(-0.49,1,1)} & \color{green}{[2,4,6]} \\ \color{green}{10:} & \color{green}{(1,-0.49,1)} & \color{green}{[0,4,6]} \\ \color{green}{11:} & \color{green}{(1,-0.09,-1)} & \color{green}{[0,5,6]} \\ \end{array} \right.$$ $$Edges~\left\{ \begin{array}{rll} \color{blue}{0:} & \color{blue}{(0,9)} & \color{blue}{[2,4]} \\ \color{blue}{1:} & \color{blue}{(0,10)} & \color{blue}{[0,4]} \\ 3: & (1,3) & [1,4] \\ 4: & (1,5) & [1,2] \\ 5: & (2,3) & [3,4] \\ 6: & (2,6) & [0,3] \\ 7: & (3,7) & [1,3] \\ \color{blue}{8:} & \color{blue}{(4,8)} & \color{blue}{[2,5]} \\ \color{blue}{9:} & \color{blue}{(4,11)} & \color{blue}{[0,5]} \\ 10: & (5,7) & [1,5] \\ 11: & (6,7) & [3,5] \\ \color{green}{12:} & \color{green}{(8,9)} & \color{green}{[2,6]} \\ \color{green}{13:} & \color{green}{(9,10)} & \color{green}{[4,6]} \\ \color{green}{14:} & \color{green}{(10,11)} & \color{green}{[0,6]} \\ \color{green}{15:} & \color{green}{(8,11)} & \color{green}{[5,6]} \\ \end{array} \right.$$
One thing I really like about this is that except for testing the vertices to see if they are in the updated polyhedron and finding where an edge crosss the plane which bounds the half space being subtracted, all the operations are on sets of integers. So this can be easily implemented for any dimension $k$. The index set of a vertex has at least $k$ elements. Edges always have $k-1$ indices. I've shown a three dimensional cube in three dimensional space. The vertices could have more than $k$ coordinates, so the cube could be embedded in a higher dimensional space.
This is also a way of generating polyhedra with particular symmetries. The equilateral triangle is invariant to 120 degree rotations about it's center, so if you start with a single half plane ${\bf u}.\hat{\bf e}_x=1$ there must be a half plane with normals $\cos( n \pi/3) \hat{\bf e}_x + \cos( n \pi/3) \hat{\bf e}_y$.
Summary
The polyhedra are stored as a list of labeled half spaces, a list of labeled vertices each with a set of at least $k+1$ half space labels denoting the planes the vertex lie on, and a list of edges with a pair of vertex labels and a set of $k$ half space labels. To subtract a half space the new half space is assigned a label and added to the list. Then the vertices are checked. and marked if they lie outside the new halfspace. Next a new vertex is added on each edge with one vertex marked and the other unmarked. The new vertex has the half space labels from the edge plus the label of the new half space. Then the index sets of the newly added vertices are checked, and if they have $k$ indices in common an edge is added with the common indices. Finally edges with both vertices unmarked and unmarked vertices are discarded.