Continuation Methods for Manifolds
There is a large class of surfaces which don't have a global parameterization without singularities. A Manifold $M$ is a set of points which can be locally parameterized. These local parameterizations can be collected into an atlas, whose union covers some finite piece of $M$. Assumming that a local parameterization can be found near a point on $M$, continuation methods are a way to build an atlas.
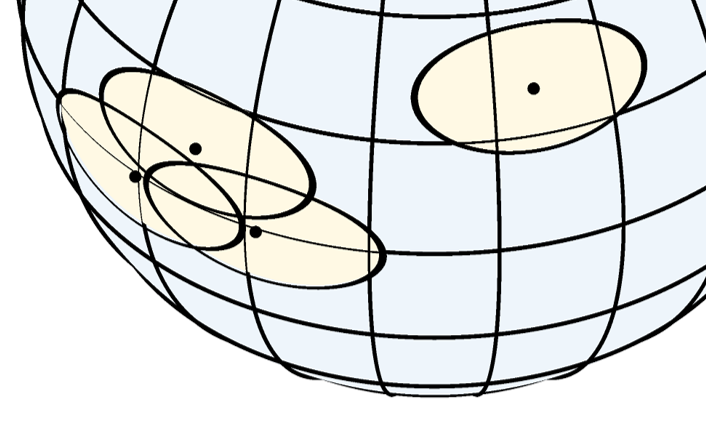
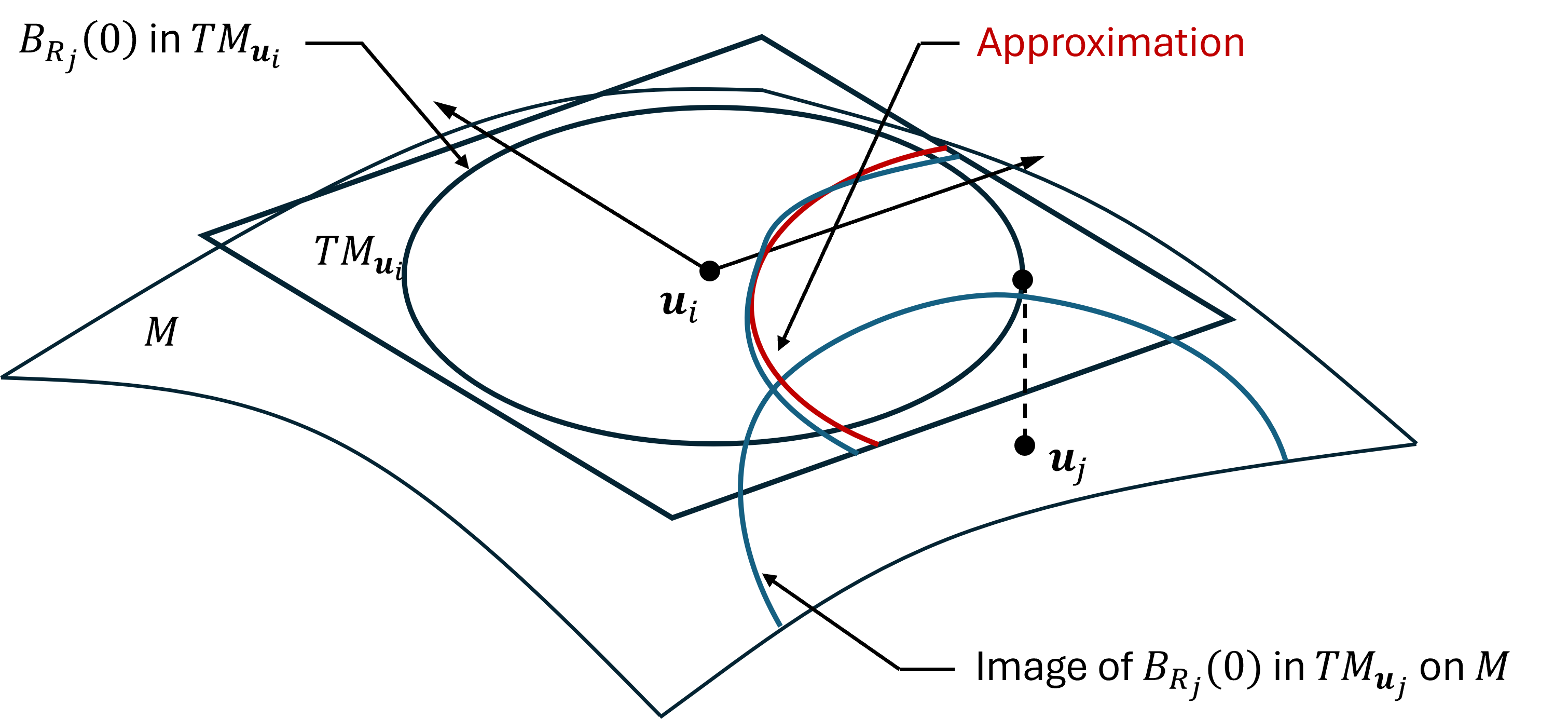
We start with a set of initial points on a $k$ dimensional manifold $M$, and some way of making a chart of $M$ near point on $M$. At minimum that means determining a radius $R$ so that any point within a ball $B_R(0)$ of radius $R$ centered at the origin of $R^k$ can be mapped to $M$.
The initial points are used to make charts of nearby points and collected into an initial atlas. The atlas should include, for each chart, a list of the charts (if any) which overlap it and which part of the charts overlap. To extend the atlas, a point in one of the charts is chosen, projected onto $M$ and the part of $M$ near this point charted and the chart added to the atlas.
If the new chart contains previously uncharted parts of $M$, the size of the part of $M$ covered by the atlas increases, and if $M$ is finite the procedure will terminate. And of course, if $M$ is infinite we need to restrict ourselves to a finite part of $M$. We don't know anything about points which do not lie in one of the charts, and creating a chart near a point in the middle of a chart may duplicate what has already been charted. The obvious choice is to choose a point on the boundary of the charted part of $M$ (the union of the charts in the atlas). Roughly half of the volume of the new chart will then be outside the union.
The boundary of a union
The boundary of a union of sets can be a complicated. It is $k-1$ dimensional, but may have more than one connected component, and those may not have continuous derivatives. This makes the boundary difficult to represent. Fortunately there is a way.
The boundary of the union of two sets $A$ and $B$ can be written as two parts $$\partial \left( A \bigcup B \right) = \left( \partial A - B \right) \bigcup \left( \partial B - A \right)$$
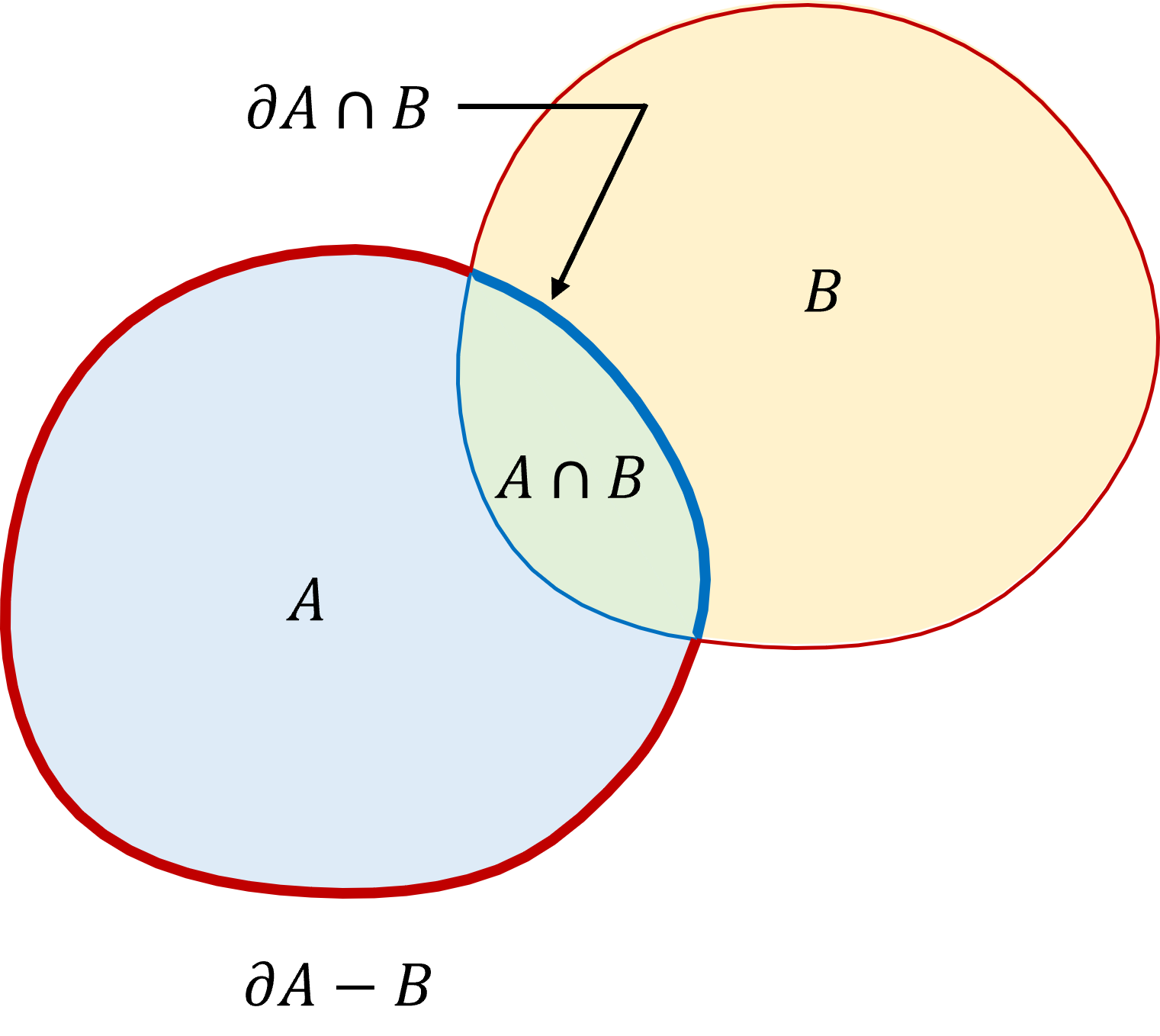
A point on the boundary can't be exterior to both the sets, it must be interior or on the boundary of one. It can't be interior to either of the two, so it must lie on the boundary of one, but not in the other.
By letting $B$ be the union of two sets this idea can be extended recursively to a finite set of sets with one part for each set $$\partial \left( \bigcup_i A_i \right) = \bigcup_i \left( \partial A_i - \bigcup_{j\neq i} A_j \right)$$
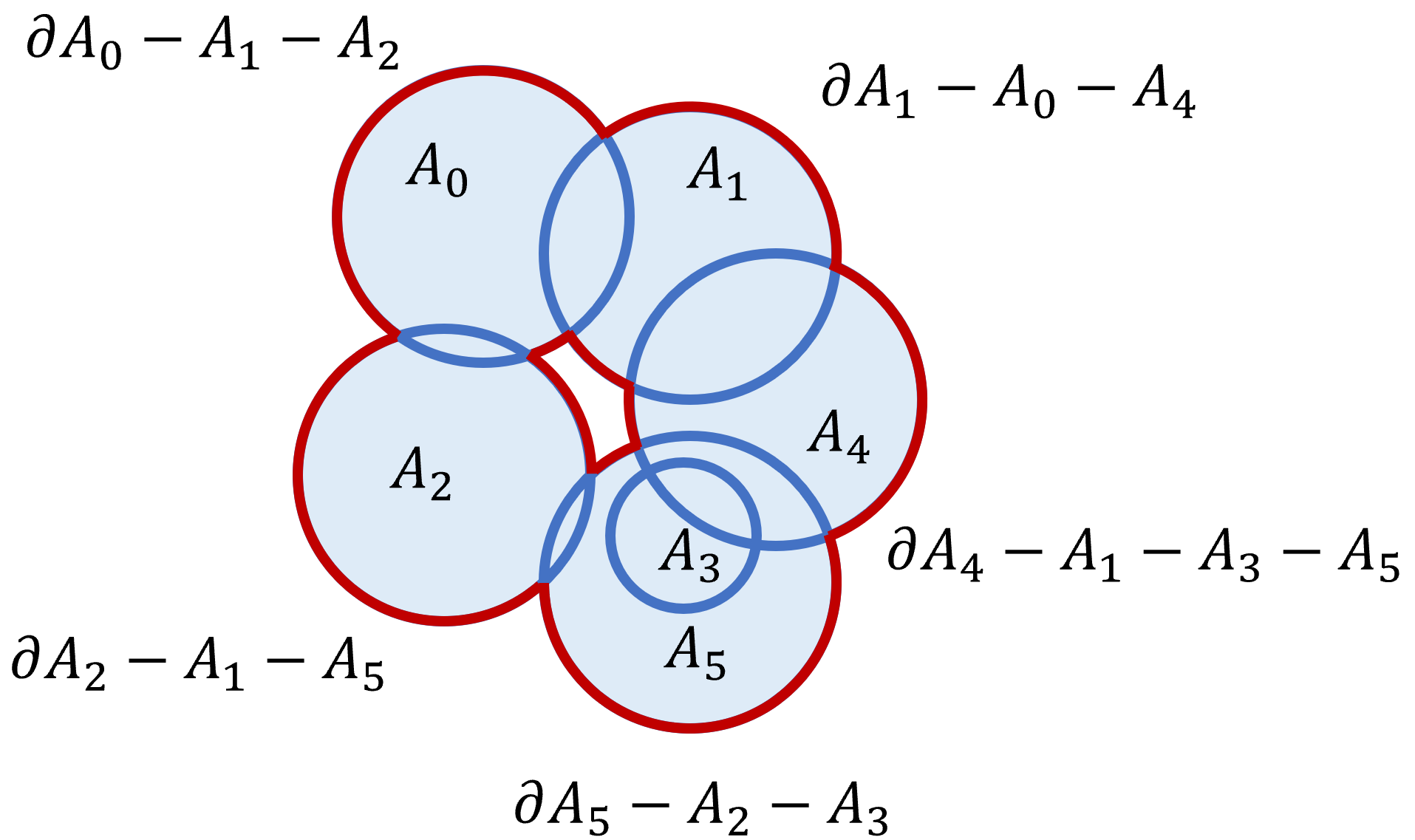
This is a representation of the boundary of a union as a list of parts of the boundary of each member, with the part of the boundary lying in another set removed. Some of these, like $A_3$ may be empty.
Lists are easy to store, but how do we represent the part of the boundary of a set that isn't interior to a bunch of other sets? They are $k-1$ dimensional surfaces, but even for simple sets like spherical balls they can have holes, several connected components, their boundary can sharp corners.
The boundary of a union of spherical balls
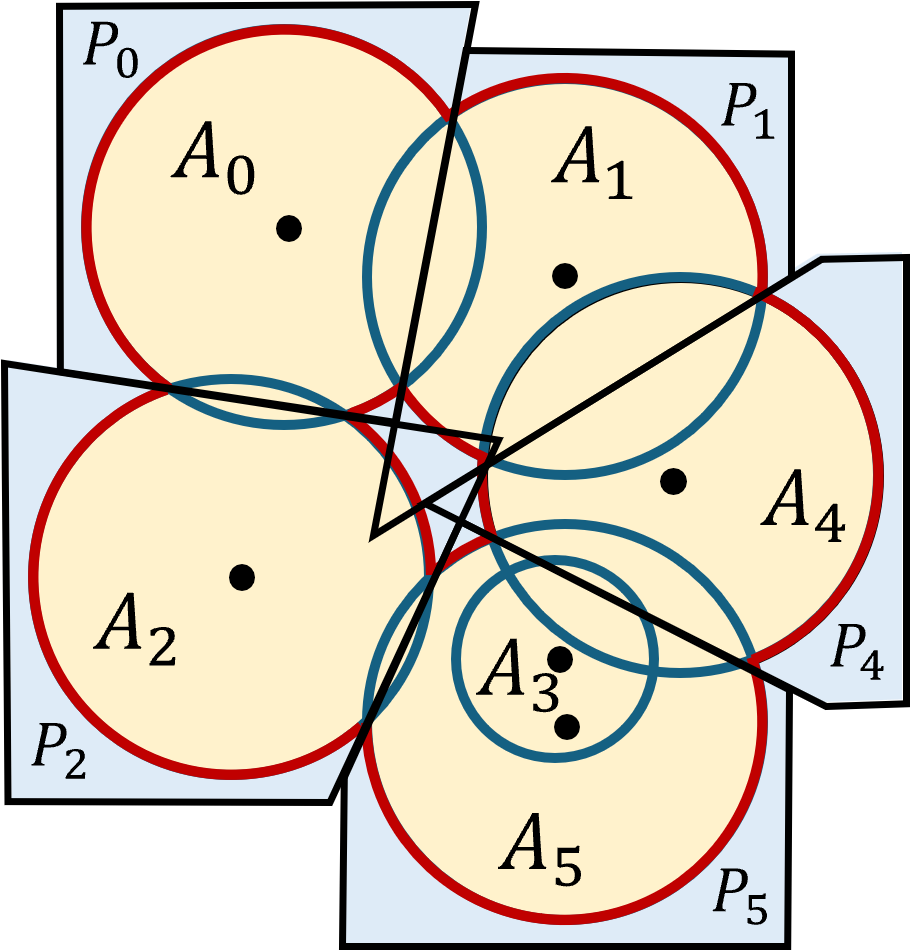
It turns out that if the sets are spherical balls $$ B_R({\bf u})=\left\{ {\bf v}~|~({\bf v}-{\bf u}).({\bf v}-{\bf u})\leq R^2\right\}$$ the pieces can be represented as the intersection of the sphere with a finite convex polyhedron. $$ \delta B_{R_i}({\bf u}_i) - \bigcup_{j\neq i} B_{R_j}({\bf u}_j) = \delta B_{R_i}({\bf u}_i) \bigcap P_i.$$ This is because of the symmetry of a pair of balls about the line connecting their centers. The part of one ball that lies outside another is the part in a half space defined by a plane which is orthogonal to the line between the centers.
This observation reduces the problem of finding a point on the boundary of a union of spherical balls to the two steps:
- finding a ball in the union whose polyhedron has a vertex outside the ball,
- finding a point on the sphere which lies inside the polyhedron.
Because adding balls to the union removes half spaces from the polyhedron, once all of the vertices are inside the ball they remain inside. The first step can be done by keeping a list of balls which lie on the boundary (their polyheddra have an external vertex) and remove them from the list if the vertices are found to all be interior. The second step can usually be done by finding where a line from the center of the ball to the exterior polyhedral vertex crosses the boundary of the ball.
Of course, using spherical balls as the chart domains doesn't translate to spherical balls on the manifold. This is an additional assumption and approximation. In a chart the domain can be chosen to be a spherical ball. The projection of the domains of neighboring charts involves projecting a spherical ball onto the manifold and then back up to the tangent space. If (and this is an assumption) the chart mapping approximately preserves distances (distances on $M$ are almost the same as distances in the tangent space), then a spherical ball in the tangent space of a nearby chart is approximately a ball in this tangent space. While this depends on the particular manifold and projection, if the tangents (in the embedding space) are orthonormal and the projection is orthogonal to the tangents space, this will be true.
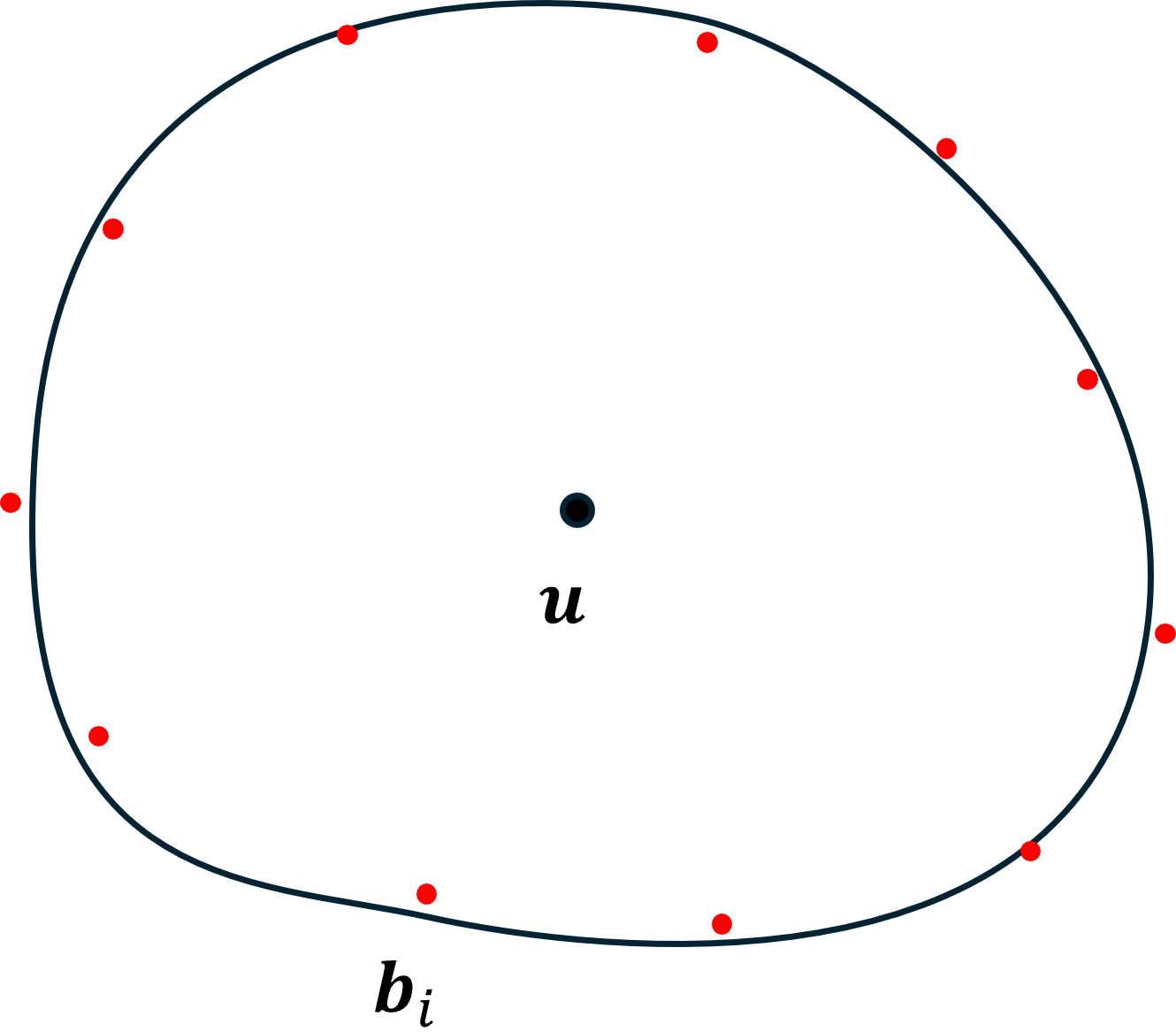
The boundary of a union using sampled points
There are other ways to represent the boundary of the union. We might distribute points ${\bf b}_i$ on the boundary of chart domains in the tangent space as the charts are created,
and test each point to see if it lies in an overlapping chart.
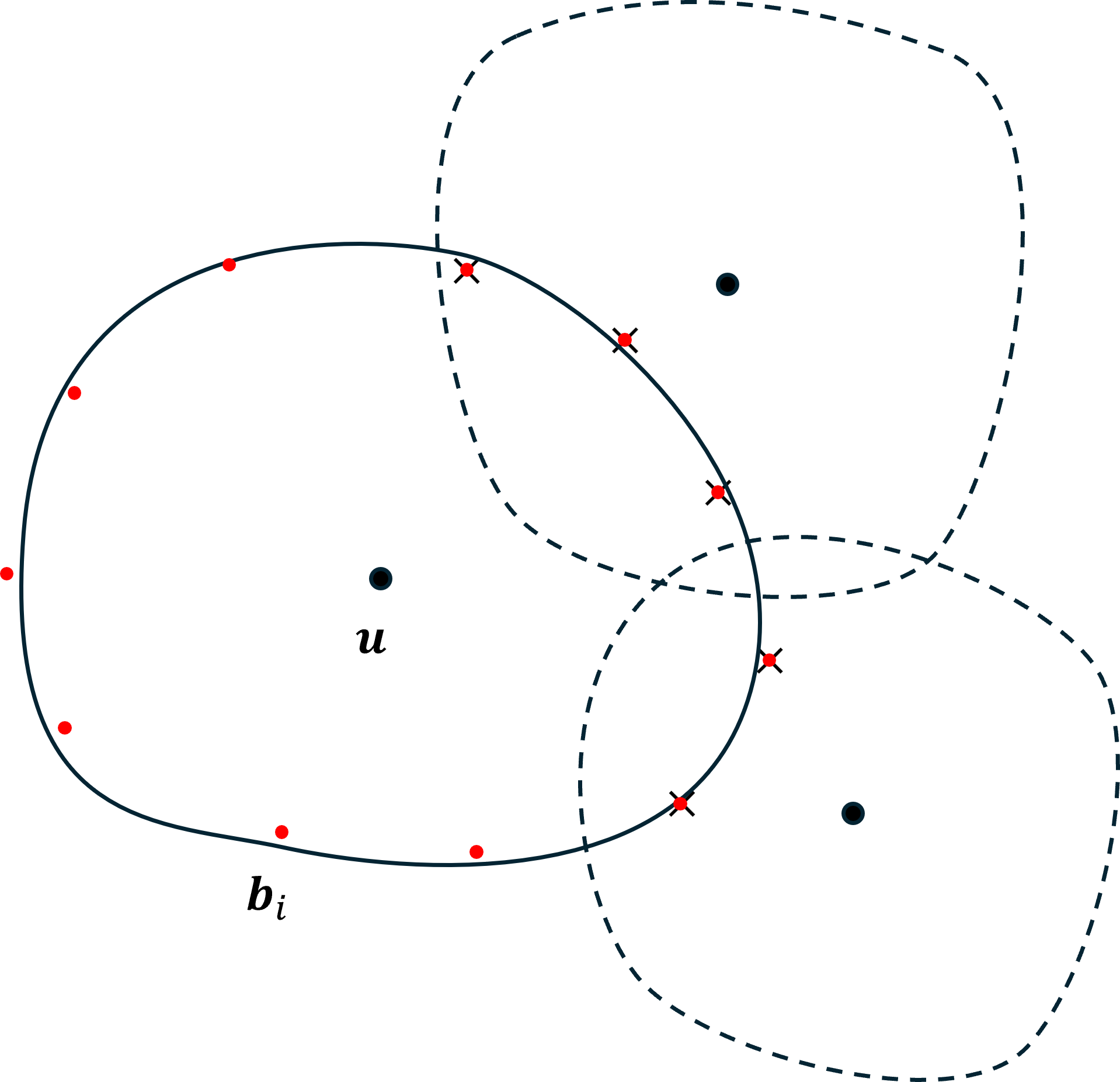
Each chart would store a list of points on its boundary, and as an overlapping chart is added those inside the new chart would be removed from the list. Assuming that the sample is dense enough, If there the list list of boundary points is empty the chart is interior to the union. Choosing a point on the boundary is just a matter of finding a cahrt with a list that's not empty and selecting any point.
If generating the points on the boundary of a chart is too difficult, points could be distributed throughout the chart domain and those near the boundary kept.
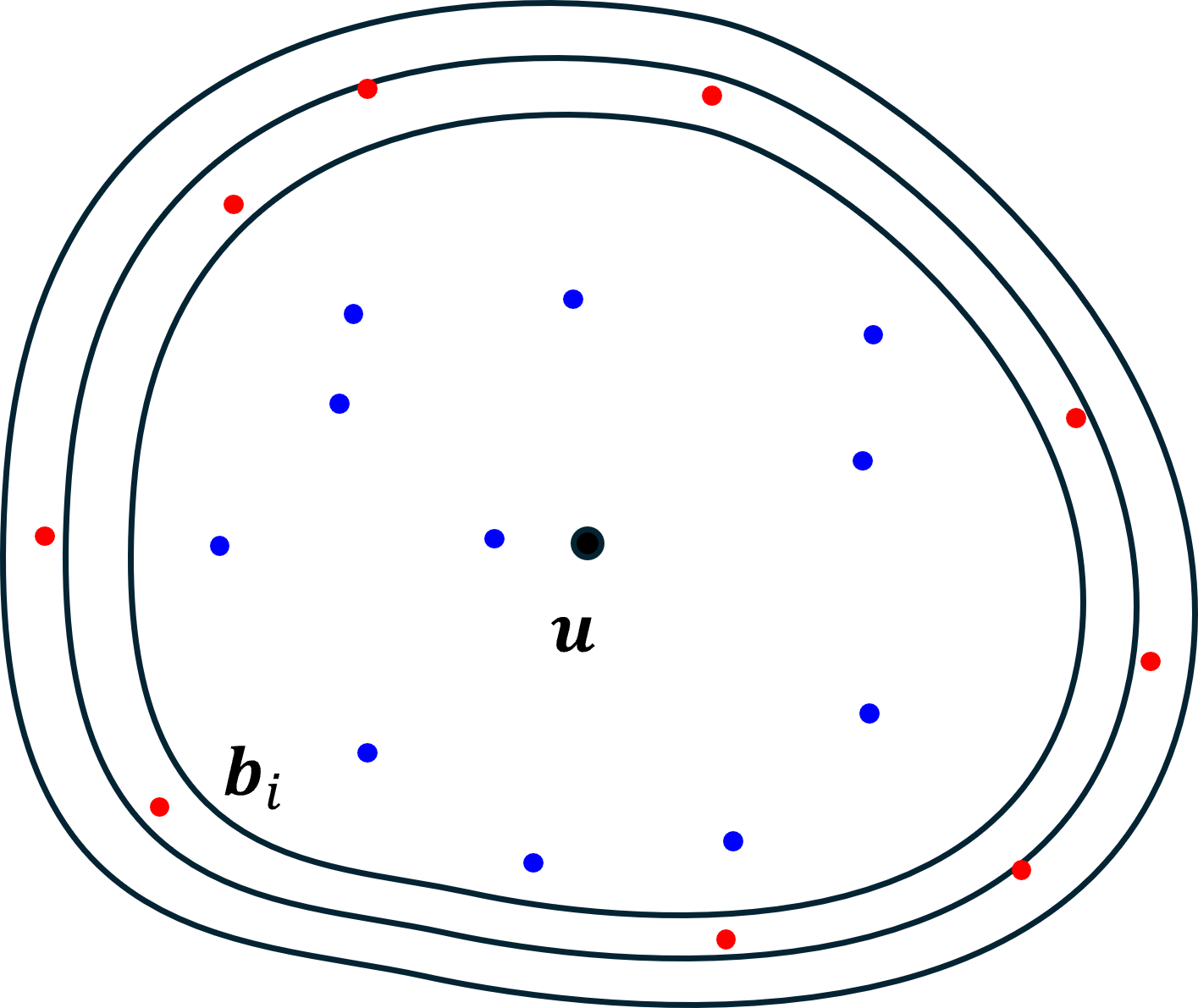
This is natural for point clouds, which are already lists of points. It does rely on being able to generate, or already having, evenly distributed points. Doing that on a closed curve is easy. It is a little more difficult on higher dimensional surfaces, but a continuation would work, if that's not too meta. If the charts are all a similar same shape this could be done beforehand. Testing points requires being able to move from one tangent space to another, which might be done by projecting them onto $M$ and then back up to the adjacent tangent space.
Path following
For one dimensional manifolds $k=1$ the algorithm is particularly simple, and you hardly need the formalism. A neighborhood of a point on a curve is a small arc, and it has two endpoints. The ball and polyhedra are both intervals on the tangent line, initially with the polyhedron's interval being slightly larger than the ball. A union of overlapping neighborhoods also has two end points, and an interval about one end point will contain that end point of the union and have one end point inside the union. Adding the new arc to the atlas removes the end point of the union and adds the exterior end point of the new interval. This looks like adding a new point off the end of the curve segment.

The boundary of a union
We have applied the algorithm to several types of manifolds. We need to be able to find tangents and to project onto the manifold. This depends on how the manifold is represented. We have considered Implicitly Defined Manifolds, Invariant Manifolds, and Point Cloud Manifolds.