Multifario Animations

Click on the image to load the animation.


Implicitly Defined Manifolds
"Multiple parameter continuation: Computing implicitly defined surfaces", IJBC, 12, pp. 451-476, 2002.

$k=1$, $n=1$:	$k=1$, $n=2$:

Line $$F(x)=0,~\forall x$$	Circle $$x^2+y^2-1=0$$
$k=2$, $n=2$:	$k=2$, $n=3$:	$k=2$, $n=3$:

Plane $$F(x,y)=0,~\forall x,y$$	Sphere $$x^2+y^2+z^2-1=0$$	Torus $${(\sqrt{x^2+y^2}-0.8)}^2+z^2-{(.5)}^2=0$$

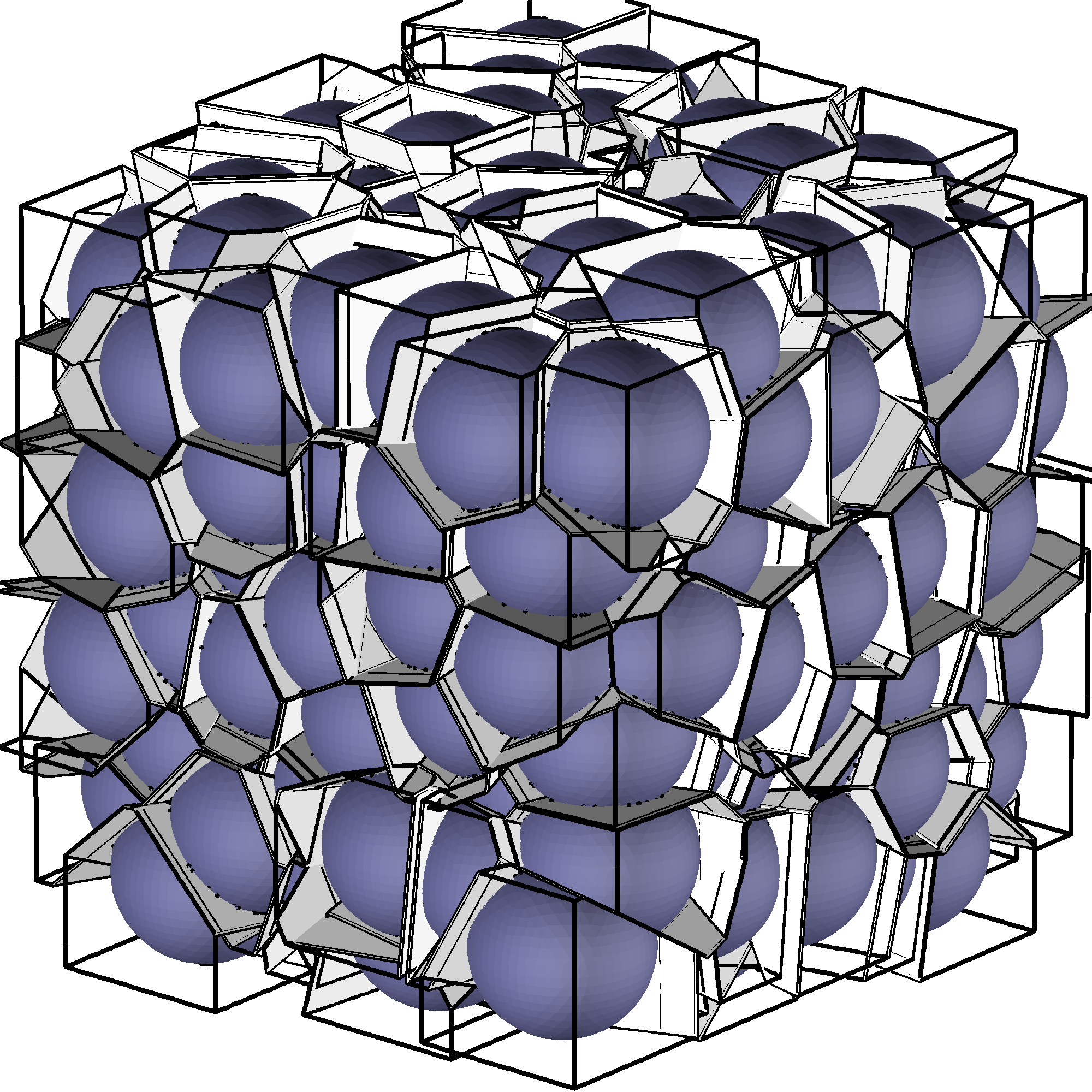
$k=3$, $n=3$:

Cube $$F(x,y,z)=0,~\forall x,y,z$$

Point Cloud Continuation
"Point Cloud Continuation: Extracting Manifolds from Observations of a Dynamical Systems", 2024. Submitted to SIADS.

$k=2$, $n=128$:	$k=2$, $n=4$:

Korteweg de Vries $$ 6 u_t+u_{xx}+9uu_x=0$$ $$u(0,t)=u(1,t)$$ $$u_x(0,t)=u_x(1,t)$$	Double Hopf Model $${d x_1}/{d t} = \alpha x_1+\beta y_1-x_1 (x_1^2 +y_1^2) + \delta (x_2-x_1+y_2-y_1)$$ $${d y_1}/{d t} =-\beta x_1+\alpha y_1-y_1 (x_1^2 +y_1^2) + \delta (x_2-x_1+y_2-y_1)$$ $${d x_2}/{d t} = \alpha x_2+\beta y_2-x_2 (x_2^2 +y_2^2) + \delta (x_1-x_2+y_1-y_2)$$ $${d y_2}/{d t} =-\beta x_2+\alpha y_2-y_2 (x_2^2 +y_2^2) + \delta (x_1-x_2+y_1-y_2)$$