Henderson, Michael E., "Multiple Parameter Continuation: Computing Implicitly Defined k-manifolds", IJBC v12(3), pages 451-76.First, multifario is a "Continuation Method", sometimes called "Numerical Continuation". Nonlinear problems are difficult to solve globally (i.e. all solutions). Locally things are much better, and for many classes of nonlinear problems a local approximation to the solution can be found. Continuation Methods attempt to build a global solution by piecing together these local approximations. They start with a "known" solution, and by finding iteratively finding solutions near a known point, cover a "component" (all solutions connected to the known solution).
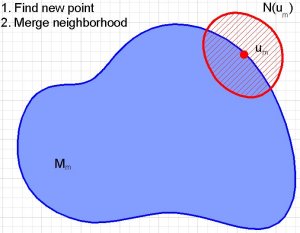
If we have a set of points and local approximations (which cover a small piece of the manifold near the point) it is clear that the next point should be near the boundary of the union of the part of the manifold covered by all the approximations. This way roughly half of the new approximation covers manifold that was not previously known.

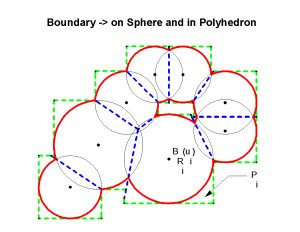
So how do we find a point on the boundary of a union of neighborhoods of points on a manifold? It doesn't sound easy, but if the neighborhoods are the projection of spherical balls in the tangent space at the point, there is an easily implemented algorithm for finding such a point. Here is a sketch of the boundary of a union:
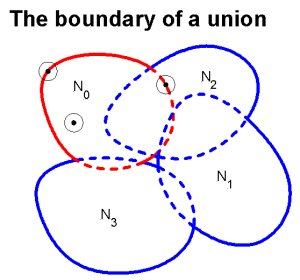
While this can be done in 2d for neighborhoods whose boundaries are single curves, in higher dimensions it is not feasible. So lets look at the subtractions, and do them pairwise, and intersect the results:
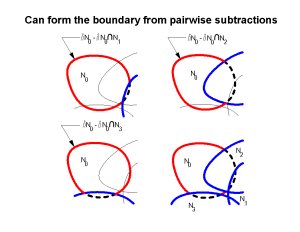
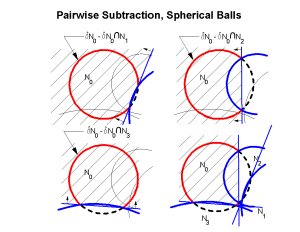
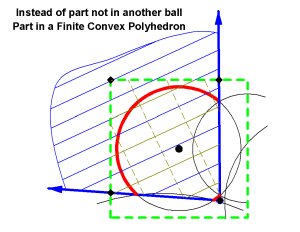
So, now all we have to do is find the part of the sphere in the polyhedron formed by intersecting these half spaces (this works in any dimension!). And, since the polyhedron outside the ball is immaterial to the result, we can start with a cube containing the ball and subtract half spaces to get a convex, finite polyhedron, and the part of the sphere which lies inside this polyhedron is the part that is on the boundary of the union.
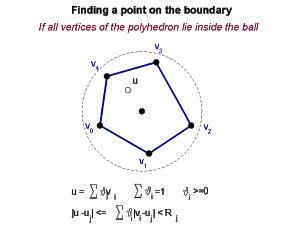
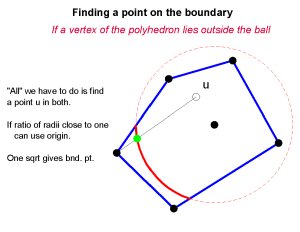
But how do we find a point on the boundary? Well, it depends on the vertices of the polyhedron. If all the vertices are inside the ball the intersection with the sphere is empty, and there is no part on the boundary. If one vertex is outside the ball, and we can find one point inside a line between the two crosses the sphere at a point that is on the boundary. And if the ratio of the radii of adjacent balls is between sqrt(2) and 1/sqrt(2) the center of the ball is inside the polyhedron, so this is a simple operation.
OK, but this is for flat "surfaces". Not very interesting (well, I find it interesting. Go stare at the animation:) If the balls are small enough relative to the curvature of the manifold the flat surface picture is pretty close to being right, and we can find the polyhedron by projecting all the adjacent balls into the tangent space the polyhedron lives in.
There. That's it. The manifold is represented by a list of points. Each
has a tangent space, a ball (just a radius), and a polyhedron (begins as
a cube slightly larger than the ball).
To find a point near the boundary we find a polyhedron with a vertex outside it's ball (keep a list of such balls, and take the first off the list - new balls get added to the list, when the first ball has no such vertices remove it from the list). The new point is actually in the tangent space of the manifold, and somehow must be projected onto the manifold.The only "hard" part is finding a point on the manifold, it's tangent plane, and an estimate for the curvature (to get the radius). For implicitly defined manifold this is "easy". Newton's method can be used to project orthogonal to the tangent space onto the manifold. The tangent space is the null space of the Jacobian, and the radius can be estimated by the distance between the point from Newton's method and the tangent plane, and from the number of Newton steps needed.To add a new ball, add the ball/polyhedron to the list, and to the list of balls that may have a boundary. Then find all the nearby balls (using hierarchical bounding boxes make this a log(m) operation), and for each project the center into the tangent space of the new ball and subtract a half space (and vice versa).